
【题目】如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交于y轴于点H.
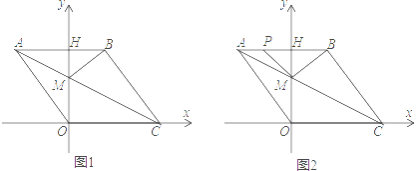
(1)连接BM,动点P从点A出发,沿折线ABC方向以1个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(2)在(1)的情况下,当点P在线段AB上运动时,是否存在以BM为腰的等腰三角形BMP?如存在,求出t的值;如不存在,请说明理由.
【答案】(1)详见解析;(2)当t=1或![]() 时,△PMB为以BM为腰的等腰三角形.
时,△PMB为以BM为腰的等腰三角形.
【解析】
(1)设点M到BC的距离为h,由△ABC的面积易得h,利用分类讨论的思想,三角形的面积公式①当P在直线AB上运动;②当P运动到直线BC上时分别得△PBM的面积;
(2)分类讨论:①当MB=MP时,PH=BH,解得t;②当BM=BP时,利用勾股定理可得BM的长,易得t.
解:
(1)设点M到BC的距离为h,
由S△ABC=S△ABM+S△BCM,
即![]() ,
,
∴h=![]() ,
,
①当P在直线AB上运动时△PBM的面积为S与P的运动时间为t秒关系为:
S=![]() (5﹣t)×
(5﹣t)×![]() ,即S=﹣
,即S=﹣![]() (0≤t<5);
(0≤t<5);
②当P运动到直线BC上时△PMB的面积为S与P的运动时间为t秒关系为:
S=![]() [5﹣(10﹣t)]×
[5﹣(10﹣t)]×![]() ,即S=
,即S=![]() t-
t-![]() (5<t≤10);
(5<t≤10);
(2)存在①当MB=MP时,
∵点A的坐标为(﹣3,4),AB=5,MB=MP,MH⊥AB,
∴PH=BH,即3﹣t=2,
∴t=1;
②当BM=BP时,即5﹣t=![]() ,
,
∴ ![]()
综上所述,当t=1或![]() 时,△PMB为以BM为腰的等腰三角形.
时,△PMB为以BM为腰的等腰三角形.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元![]() 的价格进了同样的60包茶叶,如果商家以每包
的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这些茶叶,卖完后,这家商店( )
元的价格卖出这些茶叶,卖完后,这家商店( )
A. 盈利了B. 亏损了C. 不盈不亏D. 盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A向右移动1个单位得到点B,点B向右移动(n+1)(n为正整数)个单位得到点C,点A,B,C分别表示有理数a,b,c,
(1)当n=1时,
①点A,B,C三点在数轴上的位置如图所示,a,b,c三个数的乘积为正数,数轴上原点的位置可
A.在点A左侧或在A,B两点之间 B.在点C右侧或在A,B两点之间
C.在点A左侧或在B,C两点之间 D.在点C右侧或在B,C两点之间
②若这三个数的和与其中的一个数相等,求a的值;
(2)将点C向右移动(n+2)个单位得到点D,点D表示有理数d,a、b、c、d四个数的积为正数,这四个数的和与其中的两个数的和相等,且a为整数,请在数轴上标出点D并用含n的代数式表示a.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,且∠A1B1C1=60°,对角线A1C1,B1D1相较于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2 ,使得∠B1A2D1=60°;再以A2C2为对角线作菱形A2B2C2D2,使得∠A2B2C2=60°;再以B2D2为对角线作菱形B2C3D2A3,使得∠B2A3D2=60°…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点A2018的坐标为______.
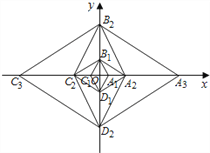
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22018的值,可令S=1+2+22+23+…+22018,则2S=2+22+23+24+…22019,因此2S﹣S=22019﹣1,即S=22019﹣1.依照以上的方法,计算出1+5+52+53+…52017的值为( )
A. 52018﹣1 B. 52019﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=![]() (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值;
(2)当t=4时,求△BMN面积;
(3)若MA⊥AB,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 是边长为4的正方形点P为OA边上任意一点(与点
是边长为4的正方形点P为OA边上任意一点(与点![]() 不重合),连接CP,过点P作
不重合),连接CP,过点P作![]() ,且
,且![]() ,过点M作
,过点M作![]() ,交
,交![]() 于点
于点![]() 联结
联结![]() ,设
,设![]() .
.
(1)当![]() 时,点
时,点![]() 的坐标为( , )
的坐标为( , )
(2)设![]() ,求出
,求出![]() 与
与![]() 的函数关系式,写出函数的定义域。
的函数关系式,写出函数的定义域。
(3)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用
的坐标(用![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
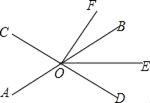
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.
(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com