
分析 (1)根据被除数=除数×商列出关系式,利用多项式相等的条件求出a,b,c的值,即可求出a-b-c的值;
(2)已知等式a5=b4,c3=d2变形表示出a与c,代入c-a=9中整理得到两个等式,相加减表示出d与b,代入已知等式求出a与b的值,即可求出a-b的值.
解答 解:(1)根据题意得:(17x2-3x+4)-(ax2+bx+c)=(17-a)x2-(b+3)x+4-c=(5x+6)(2x+1)=10x2+17x+6,
可得17-a=10,-b-3=17,4-c=6,
解得:a=7,b=-20,c=-2,
则a-b-c=7+20+2=29;
(2)由a5=b4,得:a=$\frac{{b}^{4}}{{a}^{4}}$=($\frac{{b}^{2}}{{a}^{2}}$)2,
由c3=d2,得:c=$\frac{{d}^{2}}{{c}^{2}}$=($\frac{d}{c}$)2,
代入c-a=9得:-($\frac{{b}^{2}}{{a}^{2}}$)2+($\frac{d}{c}$)2=9,
即($\frac{d}{c}$+$\frac{{b}^{2}}{{a}^{2}}$)($\frac{d}{c}$-$\frac{{b}^{2}}{{a}^{2}}$)=9,
显然,前一个括号的值大于后一个括号的值,故有$\frac{d}{c}$+$\frac{{b}^{2}}{{a}^{2}}$=9,$\frac{d}{c}$-$\frac{{b}^{2}}{{a}^{2}}$=1,
两式相加得:$\frac{d}{c}$=5,即d=5c;
两式相减得:$\frac{{b}^{2}}{{a}^{2}}$=4,即b2=4a2,
解得:b=2a,
∵a5=b4,c3=d2,
∴c3=d2=(5c)2=25c2,即c=25,d=5c=125,
由c-a=9,得a=c-9=25-9=16,b=2a=32,
则a-b=16-32=-16.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
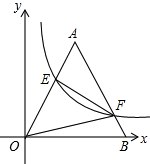 若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.
若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
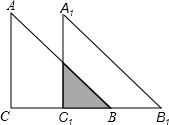 如图所示,已知ABC,∠C=90°,AC=BC=4,现将△ABC沿CB方向平移到△A1B1C1的位置.
如图所示,已知ABC,∠C=90°,AC=BC=4,现将△ABC沿CB方向平移到△A1B1C1的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com