
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100( ![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
【答案】
(1)
解:如图,作CE⊥AB于E,
由题意得:∠ABC=45°,∠BAC=60°,
设AE=x海里,
在Rt△AEC中,CE=AEtan60°= ![]() x;
x;
在Rt△BCE中,BE=CE= ![]() x.
x.
∴AE+BE=x+ ![]() x=100(
x=100( ![]() +1),
+1),
解得:x=100.
AC=2x=200.
在△ACD中,∠DAC=60°,∠ADC=75°,则∠ACD=45°.
过点D作DF⊥AC于点F,
设AF=y,则DF=CF= ![]() y,
y,
∴AC=y+ ![]() y=200,
y=200,
解得:y=100( ![]() ﹣1),
﹣1),
∴AD=2y=200( ![]() ﹣1).
﹣1).

答:A与C之间的距离AC为200海里,A与D之间的距离AD为200( ![]() ﹣1)海里.
﹣1)海里.
(2)
解:由(1)可知,DF= ![]() AF=
AF= ![]() ×100(
×100( ![]() ﹣1)≈126.3海里,
﹣1)≈126.3海里,
因为126.3>100,所以巡逻船A沿直线AC航线,在去营救的途中没有触暗礁危险.
【解析】(1)作CE⊥AB于E,设AE=x海里,则BE=CE= ![]() x海里.根据AB=AE+BE=x+
x海里.根据AB=AE+BE=x+ ![]() x=100(
x=100( ![]() +1),求得x的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;(2)根据(1)中的结论得出DF的长,再与100比较即可得到答案.
+1),求得x的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;(2)根据(1)中的结论得出DF的长,再与100比较即可得到答案.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF. 
(1)求证:△AFD≌△CEB;
(2)若∠CBE=∠BAC,四边形ABCD是怎样的四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
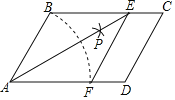
【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
求证:四边形ABEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,OC⊥OB,按下列要求利用量角器过点O作出射线OD、OE;
(1)在图①中作出射线OD满足∠COD=50°,并直接写出∠AOD的度数是 ;
(2)在图②中作出射线OD、OE,使得OD平分∠AOC,OE平分∠BOD,并求∠COE的度数;
(3)如图③,若射线OD从OA出发以每秒10°的速度绕点O顺时针方向旋转,同时射线OE从OC出发以每秒5°的速度绕点O顺时针方向旋转,设旋转的时间为t秒,在旋转过程中,当OB第一次恰好平分∠DOE时,求出t的值,并作出此时OD、OE的大概位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )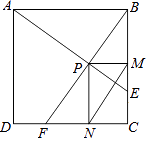
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com