
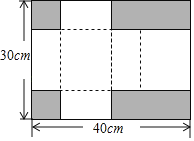
【题目】如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为_____cm3.
科目:初中数学 来源: 题型:
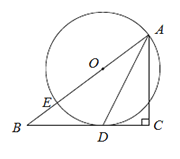
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2﹣4的图象与x轴交于点A、B(点A位于点B的左侧),C为顶点.一次函数y=mx+2的图象经过点A,与y轴交于点D.
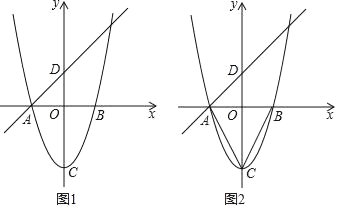
(1)求直线AD的函数表达式;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′.若新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,且当1≤x≤3时,新抛物线对应的函数值有最小值为﹣1,求新抛物线对应的函数表达式;
(3)如图,连接AC、BC,在坐标平面内,直接写出使得△ACD与△EBC相似(其中点A与点E是对应点)的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
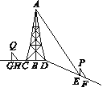
【题目】如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读资料)
同学们,我们学过用配方法解一元二次方程,也可用配方法求代数式的最值.
(1)求4x2+16x+19的最小值.
解:4x2+16x+19=4x2+16x+16+3=4(x+2)2+3
因(x+2)2大于等于0,所以4x2+16x+19大于等于3,即4x2+16x+19的最小值是3.此时,x=﹣2
(2)求﹣m2﹣m+2的最大值
解:﹣m2﹣m+2=﹣(m2+m)+2=﹣![]()
因![]() 大于等于0,所以﹣
大于等于0,所以﹣![]() 小于等于0,所以﹣
小于等于0,所以﹣![]()
![]()
小于等于![]() ,即﹣m2﹣m+2的最大值是
,即﹣m2﹣m+2的最大值是![]() ,此时,m=﹣
,此时,m=﹣![]() .
.
(探索发现)
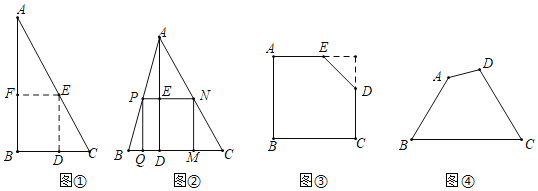
如图①,是一张直角三角形纸片,∠B=90°,AB=8,BC=6,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大.下面给出了未写完的证明,请你阅读下面的证明并写出余下的证明部分,并求出矩形的最大面积与原三角形面积的比值.
解:在AC上任取点E,作ED⊥BC,EF⊥AB,得到矩形BDEF.设EF=x
易证△AEF∽△ACB,则![]() ,
,![]() ,
,![]() ,
,![]() …
…
请你写出剩余部分
(拓展应用)
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),该矩形的面积为 .(直接写出答案)
(实际应用)
如图④,现有一块四边形的木板余料ABCD,经测量AB=70cm,BC=108cm,CD=76cm,且∠B=∠C=60°,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,该矩形的面积为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的某种商品每件的标价是![]() 元,若按标价的八折销售,仍可盈利
元,若按标价的八折销售,仍可盈利![]() ,此时该种商品每星期可卖出
,此时该种商品每星期可卖出![]() 件,市场调查发现:在八折销售的基础上,该种商品每降价
件,市场调查发现:在八折销售的基础上,该种商品每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件.设每件商品降价
件.设每件商品降价![]() 元(
元(![]() 为整数),每星期的利润为
为整数),每星期的利润为![]() 元
元
(1)求该种商品每件的进价为多少元?
(2)当售价为多少时,每星期的利润最大?最大利润是多少?
(3)2019年2月该种商品每星期的售价均为每件![]() 元,若2019年2月的利润不低于
元,若2019年2月的利润不低于![]() 元,请求出
元,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相较于A,B两点(点A在点B的左侧),且点B的坐标为(1,0)
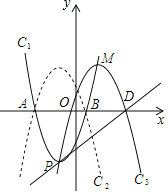
(1)求抛物线C1的函数解析式;
(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,抛物线C3的顶点为M,当点P,M关于点O成中心对称时.①求点M的坐标;②求抛物线C3的解析式;
(3)在(2)的条件下,设抛物线C3与x轴的正半轴交于点D,在直线PD的上方的抛物线C3上,是否存在点Q使得△PDQ的面积最大?若存在,求出当点Q的横坐标为何值时△PDQ面积最大,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com