
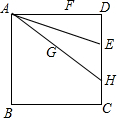
 如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.
如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$. 分析 过E作PE⊥AH于点P,设HE=x,由sin∠AHD=$\frac{AD}{AH}$=$\frac{PE}{HE}$,得$\frac{6}{AH}$=$\frac{2}{x}$,可得AH=3x,在Rt△ADH中,由AD2+DH2=AH2,可得62+(2+x)2=(3x)2,解方程即可.过G作GQ⊥AD于点Q,并反向延长交BC于点R,易得GQ=AG•sin∠DAH=$\frac{12}{5}$,推出GR=$\frac{18}{5}$,由MQ∥RN,可得$\frac{GM}{GN}$=$\frac{GQ}{GR}$=$\frac{2}{3}$,推出GM=3,MQ=$\frac{9}{5}$,由tan∠QGF=tan∠DAE=$\frac{1}{3}$,得QF=$\frac{12}{5}$×$\frac{1}{3}$=$\frac{4}{5}$,即可推出MF=$\frac{8}{5}$+$\frac{4}{5}$=$\frac{13}{5}$.
解答 解:过E作PE⊥AH于点P,设HE=x
由sin∠AHD=$\frac{AD}{AH}$=$\frac{PE}{HE}$,得$\frac{6}{AH}$=$\frac{2}{x}$,
∴AH=3x,
在Rt△ADH中,∵AD2+DH2=AH2,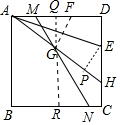
∴62+(2+x)2=(3x)2,解得x=$\frac{5}{2}$,
∴AH=$\frac{15}{2}$.
过G作GQ⊥AD于点Q,并反向延长交BC于点R,易得GQ=AG•sin∠DAH=$\frac{12}{5}$,
∴GR=$\frac{18}{5}$,
∵MQ∥RN,
∴$\frac{GM}{GN}$=$\frac{GQ}{GR}$=$\frac{2}{3}$,
∴GM=3,
∴MQ=$\frac{9}{5}$,由tan∠QGF=tan∠DAE=$\frac{1}{3}$,得QF=$\frac{12}{5}$×$\frac{1}{3}$=$\frac{4}{5}$,
∴MF=$\frac{8}{5}$+$\frac{4}{5}$=$\frac{13}{5}$.
故答案为$\frac{15}{2}$或$\frac{13}{5}$.
点评 本题考查正方形的性质、轴对称变换、锐角三角函数、勾股定理、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
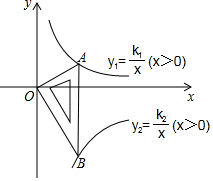 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.
如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
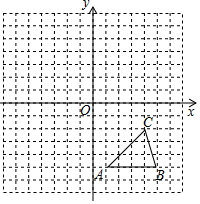 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
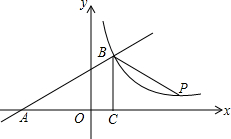 如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.
如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
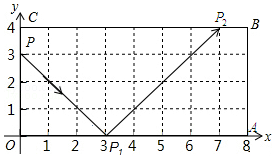 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是(5,0);点P125的坐标是(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com