练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在ABCD中，点E、F分别在边AB和CD上，下列条件不能判定四边形DEBF一定是平行四边形的是（ ）

    A.AE＝CFB.DE＝BFC.∠ADE＝∠CBFD.∠AED＝∠CFB

    【答案】B

    【解析】

    根据平行四边形的判定方法一一判断即可；

    解：A、由AE＝CF，可以推出DF＝EB，结合DF∥EB，可得四边形DEBF是平行四边形；

    B、由DE＝BF，不能推出四边形DEBF是平行四边形，有可能是等腰梯形；

    C、由∠ADE＝∠CBF，可以推出△ADE≌△CBF，推出DF＝EB，结合DF∥EB，可得四边形DEBF是平行四边形；

    D、由∠AED＝∠CFB，可以推出△ADE≌△CBF，推出DF＝EB，结合DF∥EB，可得四边形DEBF是平行四边形；

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点B，C，D都在⊙O上，过C点作CA∥BD交OD的延长线于点A，连接BC，∠B=∠A=30°，BD=2 ．

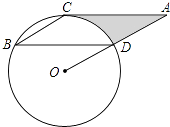
    （1）求证：AC是⊙O的切线；
    （2）求由线段AC、AD与弧CD所围成的阴影部分的面积．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，四边形中，于点，．点为边上一点，以为边作平行四边形，则最小值是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】温度的变化是人们经常谈论的话题，请根据图象与同伴讨论某天温度变化的情况．

    (1)这一天的最高温度是多少？是在几时到达的？最低温度呢？

    (2)这一天的温差是多少？从最低温度到最高温度经过多长时间？

    (3)在什么时间范围内温度在上升？在什么时间范围内温度在下降？

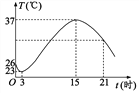
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，△ABO的顶点坐标分别为O（0，0）、A（2a，0）、B（0，﹣a），线段EF两端点坐标为E（﹣m，a+1），F（﹣m，1）（2a＞m＞a）；直线l∥y轴交x轴于P（a，0），且线段EF与CD关于y轴对称，线段CD与NM关于直线l对称．

    （1）求点N、M的坐标（用含m、a的代数式表示）；

    （2）△ABO与△MFE通过平移能重合吗？能与不能都要说明其理由，若能请你说出一个平移方案（平移的单位数用m、a表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，对角线 AC、BD 相交成的锐角α=30°，若 AC=8，BD=6，则□ABCD的面积是( )

    A.6B.8C.10D.12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，点 D 是边 BC 上的点（与 B、C 两点不重合），过点 D作 DE∥AC，DF∥AB，分别交 AB、AC 于 E、F 两点，下列说法正确的是（ ）

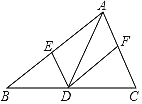
    A. 若 AD 平分∠BAC，则四边形 AEDF 是菱形

    B. 若 BD＝CD，则四边形 AEDF 是菱形

    C. 若 AD 垂直平分 BC，则四边形 AEDF 是矩形

    D. 若 AD⊥BC，则四边形 AEDF 是矩形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平行四边形ABCD中，EF过对角线的交点O，如果AB=6cm，AD=5cm，OF=2cm，那么四边形 BCEF的周长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．
    如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D；若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B；…
    设游戏者从圈A起跳．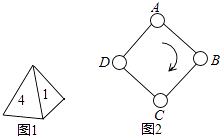

    （1）嘉嘉随机掷一次骰子，求落回到圈A的概率P1；
    （2）淇淇随机掷两次骰子，用列表法求最后落回到圈A的概率P2 ， 并指出她与嘉嘉落回到圈A的可能性一样吗？

    查看答案和解析>>

    同步练习册答案