Question

周长为24，各边长互不相等且都是整数的三角形共有多少个？

 

Answer 1

【答案】

7个

【解析】

试题分析：不妨设三角形三边为a、b、c，且a＜b＜c，由三角形三边关系定理及题设条件可确定c的取值范围，以此作为解题的突破口．

设较大边长为a，另两边长为b，c(a＞b＞c)．

因为a＜b+c，所以2a＜a+b+c，所以．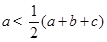

又因为2a＞b+c，所以3a＞a+b+c，所以，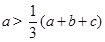

所以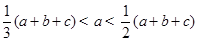．即

所以8＜a＜12，故a可为9,10,11．

满足要求的三角形共有7个（各边长见下表）

a	b	c
9	8	7
10	9	5
8	6
11	10	3
9	4
8	5
7	6

考点：本题考查的是一元一次不等式组的应用

点评：此题主要考查学生对三角形三边关系定理的理解及运用，注意写出具体三角形的三边时，结合已知条件做到不重复不遗漏．