
 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O是以BC边为直径的圆,点P为AC边上动点,⊙P的半径为2.设AP=x,则当x的取值范围是6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O是以BC边为直径的圆,点P为AC边上动点,⊙P的半径为2.设AP=x,则当x的取值范围是6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交. 分析 先由勾股定理用含x的代数式表示OP,再根据两圆相交时半径与圆心距之间的关系列出不等式组,从而确定x的取值范围.
解答 解:∵∠C=90°,AC=6,BC=8,⊙P的半径为2,AP=x,
∴CP=6-x,OC=4,⊙O的半径为4;
又∵⊙P与⊙O相交,
∴$\left\{\begin{array}{l}{x≤6}\\{2<\sqrt{(6-x)^{2}+{4}^{2}}<6}\end{array}\right.$,
解得:6-2$\sqrt{5}$<x≤6.
故当6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.
故答案为:6-2$\sqrt{5}$<x≤6.
点评 此题主要考查了圆与圆的位置关系与数量关系间的联系及不等式组的解法,利用两圆相交两半径与圆心距之间的关系是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 尺码(cm) | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量(双) | 1 | 2 | 2 | 5 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{A}{B}$=$\frac{A•M}{B•M}$ | B. | $\frac{A}{B}$=$\frac{A+M}{B+M}$ | C. | $\frac{A}{B}$=$\frac{{A}^{2}}{{B}^{2}}$ | D. | $\frac{A}{B}$=$\frac{A({x}^{2}+1)}{B({x}^{2}+1)}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
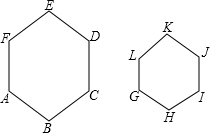 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com