
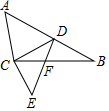
 如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且$\frac{CD}{CB}$=$\frac{3}{5}$,$\frac{CE}{AC}$=$\frac{3}{5}$.求证:△ACD∽△ECF.
如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且$\frac{CD}{CB}$=$\frac{3}{5}$,$\frac{CE}{AC}$=$\frac{3}{5}$.求证:△ACD∽△ECF. 分析 根据两边对应成比例且夹角相等,两个三角形相似求出△ACB∽△ECD,再根据相似三角形对应角相等可得∠A=∠E,利用同角的余角相等求出∠ACD=∠ECF,然后根据两角对应相等,两个三角形相似证明.
解答 证明:∵CE⊥CD,
∴∠ECD=90°,
∴∠ACB=∠ECD,
又∵$\frac{CD}{CB}$=$\frac{CE}{AC}$=$\frac{3}{5}$,
∴△ACB∽△ECD,
∴∠A=∠E,
∵∠ACB=∠ECD=90°,
∴∠ACB-∠BCD=∠ECD-∠BCD,
即∠ACD=∠ECF,
∴△ACD∽△ECF.
点评 本题考查了相似三角形的判定,相似三角形的性质,难点在于需要二次证明三角形相似,先确定出△ACB∽△ECD是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某工厂加工一种包装盒,如图所示是包装盒的表面展开图.
某工厂加工一种包装盒,如图所示是包装盒的表面展开图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
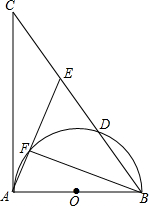 如图,在Rt△ABC中,∠BAC=90°,以AB为直径的半圆O交BC边于点D,点E在BC边上,且AE=AB,连结AE交半圆O于点F,连结BF.
如图,在Rt△ABC中,∠BAC=90°,以AB为直径的半圆O交BC边于点D,点E在BC边上,且AE=AB,连结AE交半圆O于点F,连结BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
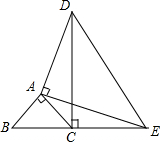 如图,AB=AC,AB⊥AC,AD=AE,AE⊥AD,B,C,E三点在同一条直线上.
如图,AB=AC,AB⊥AC,AD=AE,AE⊥AD,B,C,E三点在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
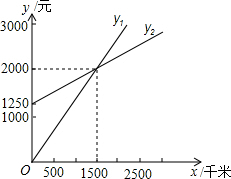 李明准备租用一辆出租车搞个体营运,现有甲乙两家出租车公司可以和他签订合同,设汽车每月行驶x千米,应付给甲公司的月租费y1元,应付给乙公司的月租费是y2元,y1、y2与x之间的函数关系的图象如图所示,请根据图象回答下列问题:
李明准备租用一辆出租车搞个体营运,现有甲乙两家出租车公司可以和他签订合同,设汽车每月行驶x千米,应付给甲公司的月租费y1元,应付给乙公司的月租费是y2元,y1、y2与x之间的函数关系的图象如图所示,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com