
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
 ,从而可知3a+
,从而可知3a+ =7,可求a,那么就可得出P、Q的坐标,再利用待定系数法可求出函数解析式;
=7,可求a,那么就可得出P、Q的坐标,再利用待定系数法可求出函数解析式; 时,点P在OA上,点Q在OB上,求三角形面积可得函数解析式;②当
时,点P在OA上,点Q在OB上,求三角形面积可得函数解析式;②当 时,点P在AC上,点Q在OB上,求三角形面积可得函数解析式;③当5
时,点P在AC上,点Q在OB上,求三角形面积可得函数解析式;③当5 时,点P、Q都在BC上,求三角形面积可得函数解析式.
时,点P、Q都在BC上,求三角形面积可得函数解析式.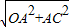 =5,(1分)
=5,(1分) ,
, ,
,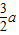 =7,
=7,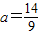 ,(4分)
,(4分) ,(5分)
,(5分) ,3),Q点坐标(
,3),Q点坐标( ,0),
,0), 解得
解得
 时,点P在OA上,点Q在OB上,
时,点P在OA上,点Q在OB上, ×OQ×OP=
×OQ×OP= ,
, 时,点P在AC上,点Q在OB上,
时,点P在AC上,点Q在OB上, ×
×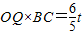 ,(4分)
,(4分) 时,点P、Q都在BC上,
时,点P、Q都在BC上,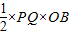 =28-
=28-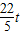 .(6分)
.(6分)

 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源:1999年全国中考数学试题汇编《三角形》(03)(解析版) 题型:解答题
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:1999年全国中考数学试题汇编《二次函数》(01)(解析版) 题型:解答题
 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
查看答案和解析>>
科目:初中数学 来源:1999年全国中考数学试题汇编《一次函数》(02)(解析版) 题型:解答题
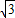 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
查看答案和解析>>
科目:初中数学 来源:1999年山东省烟台市中考数学试卷(解析版) 题型:解答题
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:1999年山东省烟台市中考数学试卷(解析版) 题型:解答题
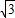 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com