
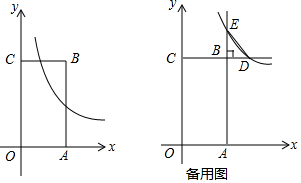
���� ��1����A��C����������B�����꣬������D�����꣬�Ӷ�����÷�������������ʽ��������E�����ꣻ
��2����k�ɷֱ��ʾ��D��E�����꣬�Ӷ��ɱ�ʾ��BD��BE�ij������á�BDE������ɵõ�����k�ķ��̣������k��ֵ��
��3������F��0��t������ɱ�ʾ��CF��CD��DF�ij����ֵ�D���߶�BC�Ϻ����߶�CB���ӳ���������������ɡ�CDF�ס�MFE���ɵ�$\frac{DF}{EF}$=$\frac{CF}{EM}$����$\frac{1-\frac{k}{2}}{2-k}$=$\frac{2-k-t+k}{1}$�����t=$\frac{3}{2}$�������ù��ɶ����з��̣������k��ֵ��������D�����꣮
��� �⣺��1�����ı���OABCΪ���Σ�A��1��0����C��0��2����
��OA=1��OC=2��
��B��1��2����
��DΪ�߶�BC���е㣬
��D��$\frac{1}{2}$��2����
�෴������������ʽΪy=$\frac{1}{x}$��
��x=1ʱ��y=1��
��E��������1��1����
��2���ɣ�1����֪OA=1��OC=2��
��D��$\frac{k}{2}$��2����E��1��k����
��BE=k-2��BD=$\frac{k}{2}$-1��
��S��BDE=$\frac{1}{2}$BD•BE=$\frac{1}{2}$��k-2����$\frac{k}{2}$-1��=$\frac{1}{16}$��
���k=$\frac{3}{2}$��k=$\frac{5}{2}$��
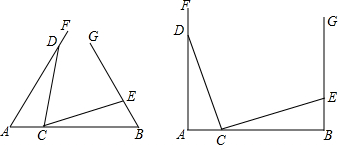
��3�����ڣ�����D���߶�BC��ʱ����E��EM��y���ڵ�M����ͼ1��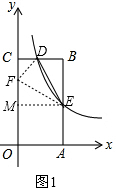
��F��0��t������OF=t��CF=2-t��
�ɣ�2������D��$\frac{k}{2}$��2����E��1��k����
��AE=OM=k��BE=2-k��CD=$\frac{k}{2}$��BD=1-$\frac{k}{2}$��MF=t-k��
�ߡ�DEF�ա�DEB��
��DF=BD=1-$\frac{k}{2}$��EF=BE=2-k��
��Rt��CDF�У��ɹ��ɶ����ɵ�CD2+CF2=DF2������$\frac{k}{2}$��2+��2-t��2=��1-$\frac{k}{2}$��2�������ɵ�k=-t2+4t-3��
�ɡ�CDF�ס�MFE���ɵ�$\frac{DF}{EF}$=$\frac{CF}{EM}$��
��$\frac{1-\frac{k}{2}}{2-k}$=$\frac{2-k-t+k}{1}$��
���t=$\frac{3}{2}$��
��k=-$\frac{9}{4}$+6-3=$\frac{3}{4}$��
��D���������$\frac{3}{8}$��2����
���� ���⿼�鷴���������ۺ��⡢���ε����ʡ�ȫ�������ε��ж������ʡ����ɶ��������������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
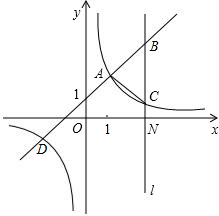 ��ͼ��һ�κ���y=kx+b��k��0���뷴��������y=$\frac{m}{x}$��m��0����ͼ���й�����A��1��2����D��-2��-1����ֱ��l��x�ᣬ��x�ύ�ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C��
��ͼ��һ�κ���y=kx+b��k��0���뷴��������y=$\frac{m}{x}$��m��0����ͼ���й�����A��1��2����D��-2��-1����ֱ��l��x�ᣬ��x�ύ�ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
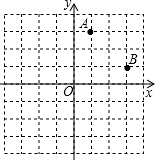 ��ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ÿ��С����ı߳�Ϊ1����λ���ȣ��ڵ�һ�������кᡢ�������Ϊ������A��B���㣮����AB�������߶�AB�Ƶ�O��˳ʱ����ת90������A1��B1��
��ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ÿ��С����ı߳�Ϊ1����λ���ȣ��ڵ�һ�������кᡢ�������Ϊ������A��B���㣮����AB�������߶�AB�Ƶ�O��˳ʱ����ת90������A1��B1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
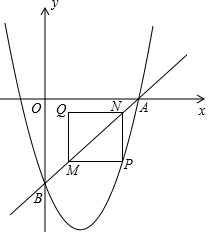 ��ͼ��ֱ��y=2x-6��������y=2x2+bx+c�ཻ��A��B���㣬��A��x���ϣ���B��y���ϣ���P��ֱ��AB�·����������ϣ���P��ֱ���PM��x�ύAB��M�㣬PN��y�ύAB��N�㣬��PM��PNΪ��������PMQN�����Q������Ϊ��m��n����
��ͼ��ֱ��y=2x-6��������y=2x2+bx+c�ཻ��A��B���㣬��A��x���ϣ���B��y���ϣ���P��ֱ��AB�·����������ϣ���P��ֱ���PM��x�ύAB��M�㣬PN��y�ύAB��N�㣬��PM��PNΪ��������PMQN�����Q������Ϊ��m��n�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
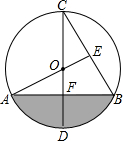 ��ͼ����֪CDΪ��O��ֱ����CD��AB������Ϊ��F����C=30�㣬����AO���ӳ���BC�ڵ�E��
��ͼ����֪CDΪ��O��ֱ����CD��AB������Ϊ��F����C=30�㣬����AO���ӳ���BC�ڵ�E���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com