
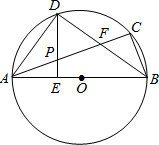
 如图,?ABC是⊙O的内接三角形,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
如图,?ABC是⊙O的内接三角形,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.分析 (1)根据角平分线的性质可得∠CBD=∠DBA,由圆周角定理可得∠DAC=∠CBD,继而可得出结论;
(2)连接OD、OC、CD,根据点D、C是半圆的三等分点,可得$\widehat{AD}$=$\widehat{CD}$=$\widehat{BC}$,CD∥AB,可得四边形OBCD为平行四边形,然后由OD=OB即可证得四边形OBCD是菱形;
(3)根据等角的余角相等,得出∠ADE=∠ABD,结合(1)可得PA=PD,再由等角的余角相等得出∠PDF=∠PFD,继而得出PD=PF,然后可得结论.
解答 解:(1)∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)连接OD、OC、CD,
∵点D、C是半圆的三等分点,
∴$\widehat{AD}$=$\widehat{CD}$=$\widehat{BC}$,CD∥AB,
∴∠AOD=∠COD=∠BOC=60°,
∴△DOC为等边三角形,
∴CD=OD=OC=OB,
∵CD∥OB,
∴四边形OBCD为平行四边形,
∵OD=OB,
∴平行四边形OBCD为菱形;
(3)∵AB为直径,
∴∠ADB=90°,
又∵DE⊥AB于点E,
∴∠DEB=90°,
∴∠ADE+∠EDB=∠ABD+∠EDB=90°,
∴∠ADE=∠ABD=∠DAP,
∴PD=PA,
又∵∠DFA+∠DAC=∠ADE+∠PDF=90°且∠ADE=∠DAP,
∴∠PDF=∠PFD,
∴PD=PF,
∴PA=PF,即P是线段AF的中点.
点评 本题考查了圆的综合应用,涉及了圆周角定理、等腰三角形的判定与性质及相似三角形的判定与性质,解答本题的关键是掌握相似三角形的对应边成比例,同弧所对的圆周角相等,注意数形结合思想运用.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 用水量(吨) | 8 | 10 | 13 | 15 | 18 |
| 费 用(元) | 16 | 20 | 29 | 35 | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.
如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中有一条线段AB,其中A(0,4),B(3,0).请你在坐标轴上找一点P,使△ABP是等腰三角形.你能找到多少符合条件的点P?在图上标出所有的点P,并写出P点的坐标.
如图,在平面直角坐标系中有一条线段AB,其中A(0,4),B(3,0).请你在坐标轴上找一点P,使△ABP是等腰三角形.你能找到多少符合条件的点P?在图上标出所有的点P,并写出P点的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com