

分析 (1)△PQR的边QR经过点B时,△ABQ构成等腰直角三角形,则有AB=AQ,由此列方程求出t的值;
(2)在图形运动的过程中,有三种情形,当1<t≤2时,当1<t≤2时,当2<t≤4时,进行分类讨论求出答案.
解答 解:(1)△PQR的边QR经过点B时,△ABQ构成等腰直角三角形,
∴AB=AQ,即3=4-t,
∴t=1.
即当t=1秒时,△PQR的边QR经过点B.
故答案为:1; (2)①当0≤t≤1时,如答图1所示.
(2)①当0≤t≤1时,如答图1所示.
设PR交BC于点G,
过点P作PH⊥BC于点H,则CH=OP=2t,GH=PH=3.
S=S矩形OABC-S梯形OPGC
=8×3-$\frac{1}{2}$(2t+2t+3)×3
=$\frac{39}{2}$-6t;
②当1<t≤2时,如答图2所示.
设PR交BC于点G,RQ交BC、AB于点S、T.
过点P作PH⊥BC于点H,则CH=OP=2t,GH=PH=3. QD=t,则AQ=AT=4-t,
QD=t,则AQ=AT=4-t,
∴BT=BS=AB-AQ=3-(4-t)=t-1.
S=S矩形OABC-S梯形OPGC-S△BST
=8×3-$\frac{1}{2}$(2t+2t+3)×3-$\frac{1}{2}$(t-1)2
=-$\frac{1}{2}$t2-5t+19;
③当2<t≤4时,如答图3所示.
设RQ与AB交于点T,则AT=AQ=4-t. PQ=12-3t,
PQ=12-3t,
∴PR=RQ=$\frac{\sqrt{2}}{2}$(12-3t).
S=S△PQR-S△AQT
=$\frac{1}{2}$PR2-$\frac{1}{2}$AQ2
=$\frac{1}{4}$(12-3t)2-$\frac{1}{2}$(4-t)2
=$\frac{7}{4}$t2-14t+28.
综上所述,S关于t的函数关系式为:
S=$\left\{\begin{array}{l}{\frac{39}{2}-6t(0≤t≤1)}\\{-\frac{1}{2}{t}^{2}-5t+19(1<t≤2)}\\{\frac{7}{4}{t}^{2}-14t+28(2<t≤4)}\end{array}\right.$.
点评 此题属于四边形综合题.考查了矩形的性质、等腰直角三角形的性质、相似三角形的判定与性质以及动点问题.注意掌握分类讨论思想的应用是解此题的关键.


科目:初中数学 来源: 题型:解答题
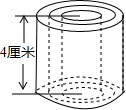 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.
如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D,若四边形ODBE的面积为8,求反比例函数解析式.
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D,若四边形ODBE的面积为8,求反比例函数解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com