
 如图,在Rt△ABC中,已知∠ACB=90°,BC=4cm,AC=9cm,点D在射线CA上从C出发向点A方向运动(点D不与点A重合),且点D运动的速度为2m/s,现设运动时间为x秒时,对应的△ABD的面积为y cm2
如图,在Rt△ABC中,已知∠ACB=90°,BC=4cm,AC=9cm,点D在射线CA上从C出发向点A方向运动(点D不与点A重合),且点D运动的速度为2m/s,现设运动时间为x秒时,对应的△ABD的面积为y cm2| 时间x秒 | … | 2 | 4 | 6 | … |
| 面积y cm2 | … | … |
分析 (1)由x的值可以找到AD的长度,套用三角形的面积公式即可得出结论;
(2)在D点的运动过程中,△ABD的面积先减少后增大,分D点在线段AC内或者CA延长线上讨论;
(3)①当临边相等的时候,三角形为等腰三角形,根据点D的运动过程能找到只有2次出现△ABD为等腰三角形,由等腰三角形底边上的高线的性质即可得出结论;②先求出△ABC的面积的$\frac{1}{4}$,套入(2)的解析式即可得出结论.
解答 解:(1)当x=2时,CD=2×2=4cm,AD=AC-CD=5cm,
此时y=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×5=10cm2.
当x=4时,CD=2×4=8cm,AD=AC-CD=1cm,
此时y=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×1=2cm2.
当x=6时,CD=2×6=12cm,AD=CD-AC=12-9=3cm,
此时y=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×3=6cm2
故答案为:10;2;6.
(2)①当D在线段AC时,如图1,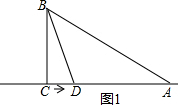
此时0<CD≤AC,即0<2x≤9,解得0<x≤$\frac{9}{2}$,
∵CD=2x,AD=AC-CD=9-2x,
∴y=$\frac{1}{2}$AD•BC=$\frac{1}{2}$(9-2x)×4=-4x+18,
∴y与x之间满足的关系式为:y=-4x+18,
②当D在CA的延长线时,如图2,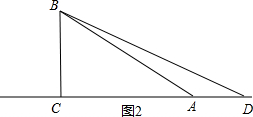
此时CD>AC,即2x>9,解得x>$\frac{9}{2}$,
∵CD=2x,AD=CD-AC=2x-9,
∴y=$\frac{1}{2}$AD•BC=$\frac{1}{2}$(2x-9)×4=4x-18;
综合①②得:y=$\left\{\begin{array}{l}{y=-4x+18(0<x≤\frac{9}{2})}\\{y=4x-18(x>\frac{9}{2})}\end{array}\right.$.
(3)①若△ABD为等腰三角形,只需AD=BD,AD=AB,或者AB=BD,
∵D点从C点出发,故当BD=AB时,AB、BD重合,不为三角形.
∴出现△ABD为等腰三角形的次数有2次.
第一次△ABD为等腰三角形时,BD=AD,
∵BD=AD,
∴过A点作BD的垂线,必平分BD.
故答案为:2;BD垂直平分线;AC.
②△ABC的面积=$\frac{1}{2}$AC×BC=$\frac{1}{2}$×9×4=18,
令y=$\frac{18}{4}$时,即$\frac{18}{4}$=-4x+18,或者$\frac{18}{4}$=4x-18,
解得x=$\frac{27}{8}$,或者x=$\frac{45}{8}$.
故当x=$\frac{27}{8}$或者x=$\frac{45}{8}$时,△ABD的面积是△ABC的面积的$\frac{1}{4}$.
点评 本题考查了动点问题的函数图象、等腰三角形的性质以及三角形的面积公式,解题的关键是(1)会用三角形的面积公式;(2)分D点在线段AC内或者CA延长线上讨论;(3)牢记等腰三角形的性质.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\frac{{\sqrt{15}}}{5}$或$\frac{{\sqrt{15}}}{3}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
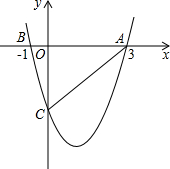 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com