
分析 如图1或2,运用分类讨论的数学思想,按FA=FD或DA=DF两种情况分类解析,分别求出AG的长度,即可解决问题.
解答 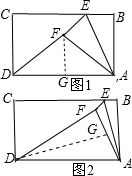 解:如图1,由题意得:
解:如图1,由题意得:
AD=BC=8,AF=AB=6;
若FA=FD,过点F作FG⊥AD于点G;
则AG=BG=4,
∴cos∠DAF=$\frac{AG}{AF}=\frac{4}{6}=\frac{2}{3}$;
如图2,若DA=DF,过点D作DG⊥AF于点G;
则AG=FG=3,cos∠DAF=$\frac{AG}{AD}$=$\frac{3}{8}$,
综上所述,该题答案为$\frac{2}{3}$或$\frac{3}{8}$.
点评 该题以矩形为载体,以考查矩形的性质、翻折变换的性质、等腰三角形的性质等几何知识点为核心构造而成;解题的关键是根据题意,正确作出符合题意的图形;灵活运用矩形的性质、翻折变换的性质等几何知识点来分析、判断、解答.


科目:初中数学 来源: 题型:解答题
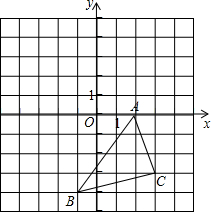 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 姓名 | 语文 | 数学 | 英语 | 政治 | 历史 |
| 小馨 | 86 | 98 | 100 | 96 | 97 |
| 小霏 | 88 | 99 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.
如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com