
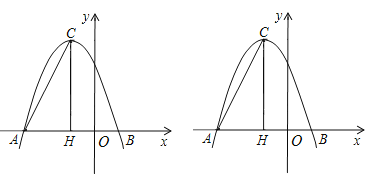
【题目】在平面直角坐标系中,抛物线![]() 与x轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写:a= ,b= ,顶点C的坐标为 ;
(2)在y轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
【答案】(1) ![]() ;C(-1,4);
;C(-1,4);
(2)点D(0,3)或(0,1);
(3) ![]() 或
或![]()
【解析】
(1)将A(-3,0)、B(1,0)代入y=ax2+bx+3求出即可,再利用平方法求出顶点坐标即可;
(2)首先证明△CED∽△DOA,得出y轴上存在点D(0,3)或(0,1),即可得出△ACD是以AC为斜边的直角三角形;
(3)首先求出直线CA的解析式为y=k1x+b1,再联立两函数解析式即可得出交点坐标,再利用若点P在对称轴左侧,只能是△PCQ∽△ACH,得∠PCQ=∠ACH得出答案即可.
解:(1)把A(-3,0)、B(1,0)分别代入y=ax2+bx+3,得
![]()
解得![]()
则该抛物线的解析式为:y=-x2-2x+3.
因为y=-x2-2x+3=-(x+1)2+4,
所以顶点C的坐标为(-1,4);
(2)如图1,假设在y轴上存在满足条件的点D,过点C作CE⊥y轴于点E.
由∠CDA=90°得∠1+∠2=90°.
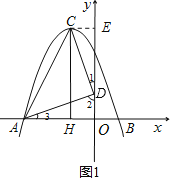
又∵∠2+∠3=90°,
∴∠3=∠1,
又∵∠CED=∠DOA=90°,
∴△CED∽△DOA,
![]()
设D(0,c),
则![]()
变形,得c2-4c+3=0,
解得c1=3,c2=1.
综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形.
(3)①若点P在对称轴右侧(如图2),只能是△PCQ∽△CAH,得∠QCP=∠CAH.
延长CP交x轴于M,
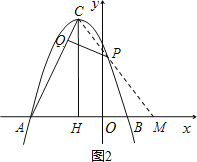
∴AM=CM,
∴AM2=CM2.
设M(m,0),则(m+3)2=42+(m+1)2,
∴m=2,即M(2,0).
设直线CM的解析式为y=k1x+b1,
则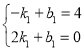
∴直线CM的解析式![]()
联立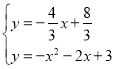
解得 或
或![]() (舍去).
(舍去).
![]()
②若点P在对称轴左侧(如图3),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
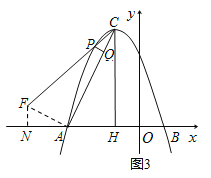
由△CFA∽△CAH得![]()
∴AN=2,FN=1,CH=4,HO=1,则AH=2,
∴点F坐标为(-5,1).
设直线CF的解析式为y=k2x+b2,则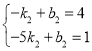
解得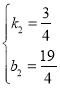
∴直线CF的解析式![]()
联立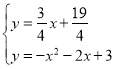
解得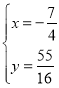 或
或![]() (舍去)
(舍去)
![]()
∴满足条件的点P坐标为![]() 或
或![]()


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
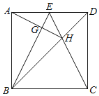
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,比如,他们研究过1,3,6,10,……,由于这些数可以用图中所示的三角形点阵标表示,他们就将其称为三角形数,第n个三角形数可以用![]() 表示.
表示.
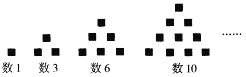
请根据以上材料,证明以下结论:
(1)任意一个三角形数乘8再加1是一个完全平方数;
(2)连续两个三角形数的和是一个完全平方数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
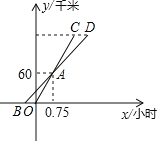
【题目】甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事,8:45才出发.甲沿相同的路线自行驾车前往,比乙早1小时到达.甲、乙两人离学校的距离y(千米)与甲出发时间x(小时)的函数关系如图所示.
(1)点A的实际意义: ,点B坐标 ;CD= ;
(2)学校与博物馆之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勤俭节约一直是中华民族的传统美德,某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛,为此先对同学们每月零花钱的数额进行一些了解,随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | a |
C | 60≤x<90 | b |
D | 90≤x<120 | 8 |
E | 120≤x<150 | 2 |
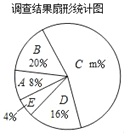
根据以上图表,解答下列问题:
(1)填空:这次调查的同学共有 人,a+b= ,m= ;
(2)求扇形统计图中扇形B的圆心角的度数;
(3)该校共有1200名学生,请估计每月零花钱的数额在60≤x<90范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
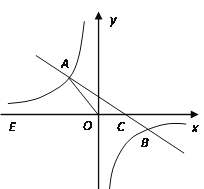
的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求△AOB 的面积;
(3)在x轴上是否存在点P,使△APC是直角三角形. 若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com