Question

3．如图：矩形ABCD中，AB=5，BC=8，点E为AD上一个动点，把△ABE沿BE折叠，点A的对应点为点F，连接DF．
（1）如图1，当点F落在矩形ABCD对角线BD上时，求$\frac{EF}{FD}$的值；
（2）连接CF，当点F落在矩形内部，tan∠FCB=$\frac{4}{5}$时，求cot∠FBC的值；
（3）当△CDF是以CF为腰的等腰三角形时，求AE的长．

Answer 1

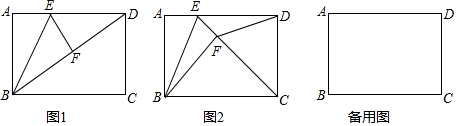
分析 （1）由折叠得：∠A=∠EFD=90°，根据同角的三角函数列式：tan∠EDF=$\frac{AB}{AD}=\frac{EF}{FD}$=$\frac{5}{8}$；
（2）作垂线，构建两个直角三角形，根据已知的三角函数设未知数：设FG=4x，GC=5x，则BG=8-5x，
在直角△BGF中利用勾股定理列方程解出即可得出结论；
（3）分两种情况：
①当FC=FD时，如图3，作辅助线，构建直角三角形，利用30°角的特殊三角函数值求得AE的长；
②当FC=DC时，如图4，作辅助线，构建直角三角形，设未知数，根据勾股定理列方程可求得AE的长．

解答 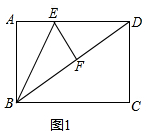解：（1）∵四边形ABCD为正方形，
∴∠A=90°，AD=BC=8，
由折叠得：∠EFB=∠A=90°，
∴∠EFD=90°，
∴tan∠EDF=$\frac{AB}{AD}=\frac{EF}{FD}$=$\frac{5}{8}$；
（2）如图2，过F作FG⊥BC于G，
∵tan∠FCB=$\frac{4}{5}$，
∴设FG=4x，GC=5x，则BG=8-5x，
∵BF=AB=5，
由勾股定理得：BF²=BG²+FG²，
5²=（4x）²+（8-5x）²，
41x²-80x+39=0，
（x-1）（41x-39）=0，
x₁=1，x₂=$\frac{39}{41}$，
当x₁=1时，FG=4x=4，BG=8-5x=3，
∴cot∠FBC=$\frac{BG}{FG}$=$\frac{3}{4}$，
当x₂=$\frac{39}{41}$时，FG=4x=$\frac{156}{41}$，BG=8-5x=8-5×$\frac{39}{41}$=$\frac{133}{41}$，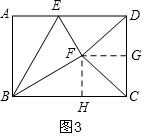
∴cot∠FBC=$\frac{BG}{FG}$=$\frac{\frac{133}{41}}{\frac{156}{41}}$=$\frac{133}{156}$，
综上所述，cot∠FBC的值为$\frac{3}{4}$或$\frac{133}{156}$；
（3）当△CDF是以CF为腰的等腰三角形时，分两种情况：
①当FC=FD时，如图3，过F作FH⊥BC于H，过F作FG⊥DC于G，
∴DG=GC=$\frac{1}{2}$DC=$\frac{5}{2}$，
∵∠FHC=∠BCD=∠FGC=90°，
∴四边形FHCG是矩形，
∴FH=CG=$\frac{5}{2}$，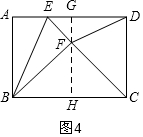
∴FH=$\frac{1}{2}$BF，
在Rt△BFH中，∠FBH=30°，
∵∠ABC=90°，
由折叠得：∠ABE=∠EBF=$\frac{90°-30°}{2}$=30°，
∴tan∠ABE=$\frac{AE}{AB}$，
∴AE=tan30°•AB=$\frac{\sqrt{3}}{3}$×5=$\frac{5\sqrt{3}}{3}$；
②当FC=DC时，如图4，过F作FG⊥BC，交BC于G，交AD于H，
∵AD∥BC，
∴GH⊥AD，
∵AB=BF，AB=CD，
∴BF=FC，
∴BG=CG=4，
由勾股定理得：FG=$\sqrt{{5}^{2}-{4}^{2}}$=3，
∵∠A=∠ABG=∠BGH=90°，
∴四边形ABGH为矩形，
∴GH=AB=5，AH=BG=4，
∴FH=5-3=2，
设AE=x，则EF=x，EH=AH-AE=4-x，
由勾股定理得：x²=（4-x）²+2²，
x=$\frac{5}{2}$，
∴AE=$\frac{5}{2}$，
综上所述，AE的长为$\frac{5\sqrt{3}}{3}$或$\frac{5}{2}$．

点评 本题是四边形的综合题，考查了矩形、等腰三角形的性质和判定、折叠的性质，本题构建直角三角形，利用勾股定理列方程是关键；难度适中，属于中考常考题型．