练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
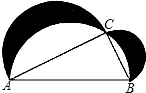
    18．如图，在Rt△ACB中，∠C=90°，AB=10、BC=6，分别以AB、BC、AC为直径作三个半圆，求阴影部分的面积．

    分析 利用勾股定理可求出AC的长，由题意可知阴影部分面积可以看成是以AC、BC为直径的两个半圆的面积加上一个直角三角形ABC的面积减去一个以AB为直径的半圆的面积．

    解答 解：∵∠C=90°，AB=10、BC=6，
    ∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8，
    ∴以AB为直径的半圆面积为12.5π，以AC为直径的半圆面积为8π，以BC为直径的半圆面积为4.5π，直角三角形ABC的面积=24，
    ∴阴影部分的面积=8π+4.5π-12.5π+24=24．

    点评 此题主要考查了扇形面积的计算公式，解题的关键是由题意读懂阴影部分的面积可以看作是几个规则图形的面积的和或差．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．下列运算正确的是（　　）
    A．32-2a2=1B．a6÷a3=a2C．（a-b）2=a2-b2D．2a•4a=8a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．若xa-b-2-2ya+b=3是二元一次方程，则a=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

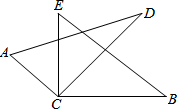    6．如图，将两块直角三角尺的直角顶点C叠放在一起，
    ①若∠DCB=35°，求ACB的度数；
    ②若∠ACB=140°，求DCE的度数；
    ③猜想∠ACB与∠DCE的大小关系，并写出你的猜想，但不要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知，在△ABC中，AB=AC，CD⊥AB于点D，BE⊥AC与点E，BE、CD相交于点F，连结AF．求证：∠BAF=∠CAF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．已知点M（-2，3）在双曲线y=$\frac{k}{x}$上，则下列各点一定在该双曲线上的是（　　）
    A．（3，-2）B．（-2，-3）C．（2，3）D．（3，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

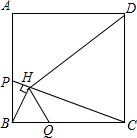    10．如图，P、Q是正方形ABCD边AB、BC上的点，BH⊥PC，垂足为H，且DH⊥HQ．
    （1）证明：$\frac{BQ}{DC}$=$\frac{BH}{CH}$；
    （2）试猜想BP与BQ的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．解不等式组，在数轴上表示出来，并写出不等式组的整数解．
    $\left\{\begin{array}{l}{3（x+1）＞4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

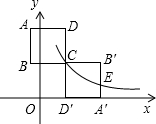    8．如图，正方形ABCD的顶点C在反比例函数y=$\frac{k}{x}$上，把该正方形绕其顶点C顺时针旋转180°，AD边恰好落在x轴正半轴上，已知A（-1，6），则k=6．

    查看答案和解析>>

    同步练习册答案