
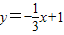 交y轴于D点,E为抛物线顶点.若∠DBC=α,∠CBE=β,求α-β的值.
交y轴于D点,E为抛物线顶点.若∠DBC=α,∠CBE=β,求α-β的值.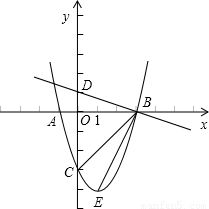
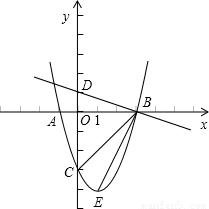 解:(I)抛物线y=ax2+bx-3与y轴交于点C(0,-3),
解:(I)抛物线y=ax2+bx-3与y轴交于点C(0,-3),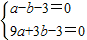 ,
, ,
,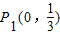 .
. ),P2(9,0),P3(0,0).
),P2(9,0),P3(0,0).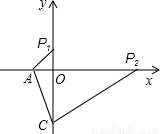
 x+1,得D(0,1)
x+1,得D(0,1)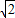 ,CE=
,CE=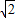 ,BE=2
,BE=2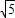 ,
,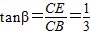 .
.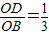 .
.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源:2009年北京市崇文区中考数学一模试卷(解析版) 题型:解答题
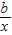 的图象都经过点(x1,kx2),求一次函数与反比例函数的解析式.
的图象都经过点(x1,kx2),求一次函数与反比例函数的解析式.查看答案和解析>>
科目:初中数学 来源:2010年中考复习针对性训练 几何探究题(解析版) 题型:解答题
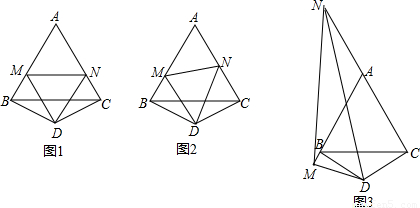
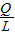 =______;
=______;查看答案和解析>>
科目:初中数学 来源:2009年北京市崇文区中考数学一模试卷(解析版) 题型:解答题
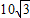 ,且∠ABC=60°,求CD的长.
,且∠ABC=60°,求CD的长.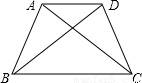
查看答案和解析>>
科目:初中数学 来源:2009年北京市崇文区中考数学一模试卷(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com