
分析 (1)分0<t≤3与3<t两种情况找出y关于x的函数关系式;
(2)代入x=2和x=6求出y值,由此即可得出结论;
(3)代入y=1.2,求出x值,此题得解.
解答 解:(1)根据题意可知:
当0<t≤3时,y=0.2;
当3<t时,y=0.2+0.1(t-3)=0.1t-0.1.
综上可知:y与x之间的函数关系式为y=$\left\{\begin{array}{l}{0.2(0<t≤3)}\\{0.1t-0.1(3<t,t为正整数)}\end{array}\right.$.
(2)当x=2时,y=0.2;
当x=6时,y=0.1×6-0.1=0.5.
答:当通话时间为2分钟时,则应交话费0.2元,当通话时间为6分钟时,则应交话费0.5元.
(3)显然当x>3时,y才有可能为1.2元.
当y=1.2时,有1.2=0.1t-0.1,
解得:t=13.
答:当应交话费1.2元时,通话时间是13分钟.
点评 本题考查了一次函数的应用,解题的关键是根据数量关系找出y关于x的函数关系式.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
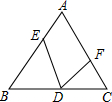 如图,在等边三角形△ABC中,点D为线段BC的中点,点E、F分别在线段AB和AC上,∠EDF=60°.
如图,在等边三角形△ABC中,点D为线段BC的中点,点E、F分别在线段AB和AC上,∠EDF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
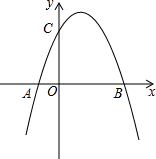 如图,将抛物线y=-x2+1平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),并与x轴交于点C.
如图,将抛物线y=-x2+1平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),并与x轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一个港湾内有M、N两个小岛,在M岛上的艄公每天早上都要用渡船把M岛上的一部分居民送到OA所在的岸,一部分居民送到OB所在的岸,然后回到N岛上休息,试问:应怎样确定两岸的停泊处,才能使渡船行驶的路程最短?画出图形说明.
如图,一个港湾内有M、N两个小岛,在M岛上的艄公每天早上都要用渡船把M岛上的一部分居民送到OA所在的岸,一部分居民送到OB所在的岸,然后回到N岛上休息,试问:应怎样确定两岸的停泊处,才能使渡船行驶的路程最短?画出图形说明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形ABCD中,点EF分别在边BC和CD上,且AE⊥BF.点C关于自线BF的对称点为点G,连线FG并延长交AD于点H,若点H是AD的三等分点,则的$\frac{BE}{BC}$值为$\frac{1}{5}$或$\frac{11}{12}$.
正方形ABCD中,点EF分别在边BC和CD上,且AE⊥BF.点C关于自线BF的对称点为点G,连线FG并延长交AD于点H,若点H是AD的三等分点,则的$\frac{BE}{BC}$值为$\frac{1}{5}$或$\frac{11}{12}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com