
已知抛物线y=ax2+c的顶点为D(0,![]() ),且过点A(1,
),且过点A(1,![]() ),如图所示.
),如图所示.

(1)试求这条抛物线的代数表达式;
(2)点F是坐标原点O关于该抛物线顶点D的对称点,坐标为(0,![]() ),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=
),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=![]() -
-![]() =
=![]() .在Rt△AFA2中,有FA=
.在Rt△AFA2中,有FA=![]() =
=![]() .
.
已知抛物线上另一点B的横坐标为2,求线段FB的长.
(3)若点P是该抛物线上在第一象限内的任意一点,试探究线段FP的长度与点P的纵坐标的大小关系,并证明你的猜想.
|
[答案](1)由已知,得
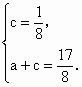 解这个方程组,得 解这个方程组,得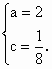
∴该抛物线的代数表达式为y=2x2+ (2)当x=2时,y=2×22+ 即点 B的坐标为(2,如图,过 B作BB1⊥x轴于点B1,过F作FB2∥x轴交BB1于点B2,则FB2=2,BB2=在 Rt△BFB2中,FB=(3)相等 设 P点的坐标为(x,y),则x>0,y>0,且y=2x2+过 P作PP1⊥x轴于P1,过F作FP2∥x轴交PP1于点P2,则FP2=x,PP2=y-在 Rt△PFP2中,FP=∴抛物线在第一象限内的任意一点P到点F的距离等于这一点P的纵坐标. [剖析]由FA、FB的长,可获得第(3)问的猜想,从FA、FB的长的求解过程可发现,求长的关键是要知道该点的坐标,故可先设出P点坐标(由于P点在第一象限,故x>0,y>0,然后用x的代数式表示FP的长度,最后由y与x的关系获得FP与y的关系. |
|
[方法提炼] 通过阅读、理解,获得一种新的方法,然后运用新方法解决问题.另外还要注意从结论和过程两个角度进行归纳,以获得一般性的结论和解法. |


科目:初中数学 来源: 题型:
已知抛物线y=ax2+bx+c(a>0)经过点B(12,0)和C(0,-6),对称轴为x=2.
(1)求该抛物线的解析式.
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若![]() 存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
标;若存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.查看答案和解析>>
科目:初中数学 来源:2012届山东邹城北宿中学九年级3月月考数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2010-2011年浙江省嵊州市九年级上学期期末考试数学卷 题型:解答题
(本小题满分14分)
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3)。设抛物线的顶点为D,求解下列问题:

1.(1)求抛物线的解析式和D点的坐标;
2.(2)过点D作DF∥ 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
3.(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com