
 如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米? 分析 过点A作AE⊥BC于点E,过点D作DF⊥AE于点F,根据∠B=45°可得出△ABE是等腰直角三角形,故可得出AE=BE,∠BAE=∠B=45°.再由∠A=75°可得出∠DAF的度数,进而可得出AF及DF的长,根据BC⊥CD可得出四边形CDFE是矩形,故可得出CD=EF,CE=DF,据此可得出结论.
解答 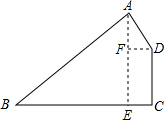 解:如图,过点A作AE⊥BC于点E,过点D作DF⊥AE于点F,
解:如图,过点A作AE⊥BC于点E,过点D作DF⊥AE于点F,
∵∠B=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,∠BAE=∠B=45°.
∵AB=500$\sqrt{2}$米,
∴AE=BE=500$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=500米.
∵∠A=75°,
∴∠DAF=75°-45°=30°.
∵AD=200米,
∴DF=$\frac{1}{2}$AD=100米,AF=200×$\frac{\sqrt{3}}{2}$=100$\sqrt{3}$米.
∵BC⊥CD,
∴四边形CDFE是矩形,
∴CD=EF=AE-AF=(500-100$\sqrt{3}$)米,CE=DF=100米,
∴AB+BC+AD+CD=500$\sqrt{2}$+(500+100)+200+(500-100$\sqrt{3}$)=(1300+500$\sqrt{2}$-100$\sqrt{3}$)米.
答:围墙的长度是(1300+500$\sqrt{2}$-100$\sqrt{3}$)米.
点评 本题考查的是勾股定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数量(辆) | 购买总费用(万元) | 载客总量(万人次) | |
| A型车 | x | 100x | 60x |
| B型车 | 10-x | 150(10-x) | 100(10-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
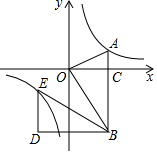 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
(1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 9 | C. | -5 | D. | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com