
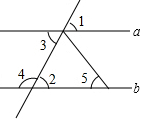
 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠3+∠4=180° | D. | ∠3=∠5 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批灯泡的使用寿命是否合格 | |
| B. | 了解珠江河中鱼的各类 | |
| C. | 了解广东电视台珠江频道《今日关注》的收视率 | |
| D. | 了解某校七年级一班学生的视力状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一样稳定 | B. | 前者比后者稳定 | C. | 后者比前者稳定 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
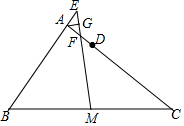 如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连结MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.
如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连结MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com