
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
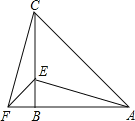
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
【答案】(1)证明见解析;(2)证明见解析;(3)60°
【解析】
试题分析:(1)根据在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,可以得到Rt△ABE和Rt△CBF全等的条件,从而可以证明Rt△ABE≌Rt△CBF;
(2)根据Rt△ABE≌Rt△CBF,可以得到AB=BC,BE=BF,然后即可转化为AB、CE、BF的关系,从而可以证明所要证明的结论;
(3)根据Rt△ABE≌Rt△CBF,AB=CB,∠CAE=30°,可以得到∠ACF的度数.
(1)证明:∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)证明:∵Rt△ABE≌Rt△CBF,
∴AB=BC,BE=BF,
∵BC=BE+CE,
∴AB=CE+BF.
(3)∵AB=CB,∠ABC=90°,∠CAE=30°,∠CAB=∠CAE+∠EAB,
∴∠BCA=∠BAC=45°,
∴∠EAB=15°,
∵Rt△ABE≌Rt△CBF,
∴∠EAB=∠FCB,
∴∠FCB=15°,
∴∠ACF=∠FCB+∠BCA=15°+45°=60°,
即∠ACF=60°.


科目:初中数学 来源: 题型:
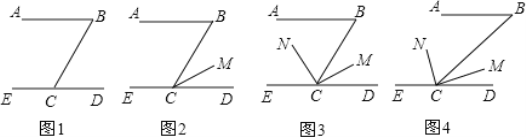
【题目】 (1)①如图1,已知AB∥CD,∠ABC=60°,可得∠BCD=_______°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=_________°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=___________°.
(2)、尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线, CN⊥CM,求∠BCM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.“打开电视机,正在播放《动物世界》”是必然事件
B.某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C.抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D.想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
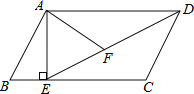
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com