
 如图在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.分析 (1)先根据圆周角定理得出AN⊥BC,再由等腰三角形的性质得出∠1=∠2,根据切线的性质得出CP⊥AC,故∠3+∠4=90°,利用等量代换可得出结论;
(2)根据等腰三角形的性质得出∠3=∠5,再由圆内接四边形的性质得出∠3+∠AMN=180°,故可得出∠AMN=∠CBP.根据∠2=∠4得出△AMN∽△CBP,由相似三角形的性质即可得出结论.
解答 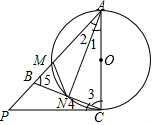 证明:(1)∵AC是⊙O的直径,
证明:(1)∵AC是⊙O的直径,
∴∠ANC=90°,
∴AN⊥BC.
又∵AB=AC,
∴∠1=∠2.
∵CP切⊙O于点C,
∴CP⊥AC,
∴∠3+∠4=90°.
∵∠1+∠3=90°,
∴∠1=∠4,
∴∠2=∠4 即∠BCP=∠BAN;
(2)∵AB=AC,
∴∠3=∠5.
又∵四边形AMNC为⊙O的内接四边形,
∴∠3+∠AMN=180°.
又∵∠5+∠CBP=180°,
∴∠AMN=∠CBP.
又∵∠2=∠4,
∴△AMN∽△CBP,
∴$\frac{AM}{MN}$=$\frac{CB}{BP}$,即AM•BP=MN•CB.
点评 本题考查的是相似三角形的判定与性质,熟知圆内接四边形的性质、切线的判定与性质等知识是解答此题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | k$≥-\frac{9}{4}$ | B. | k$>-\frac{9}{4}$ | C. | k$≥-\frac{9}{4}$且k≠0 | D. | k$>-\frac{9}{4}$且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
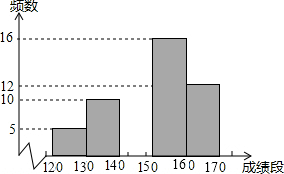 为迎接2016年初中学业水体育考试,某校从500名九年级学生中随机抽取部分学生进行1分钟跳绳测试,并把测试成绩进行分析整理,制作成如下统计图表
为迎接2016年初中学业水体育考试,某校从500名九年级学生中随机抽取部分学生进行1分钟跳绳测试,并把测试成绩进行分析整理,制作成如下统计图表| 成绩段 | 频数 | 频率 |
| 120x130 | 5 | 0.1 |
| 130x140 | 10 | A |
| 140x150 | B | 0.14 |
| 150x160 | 16 | C |
| 160x170 | 12 | 0.24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
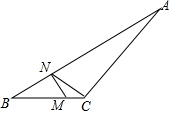 如图,在△ABC中,∠B=30°,M为BC上一点且MC:MB=m:n,MN⊥AB于N,联结CN,则cot∠CNA的值为$\frac{\sqrt{3}m}{m+n}$.
如图,在△ABC中,∠B=30°,M为BC上一点且MC:MB=m:n,MN⊥AB于N,联结CN,则cot∠CNA的值为$\frac{\sqrt{3}m}{m+n}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com