
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() .
.

(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若 ![]() 时,求点P的坐标;
时,求点P的坐标;
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG 与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由。
【答案】(1) y=-![]() (x-2)2+4.(2) P(0,2),P(0,-2).(3) y=4x+
(x-2)2+4.(2) P(0,2),P(0,-2).(3) y=4x+![]() 或y=-
或y=-![]() .
.
【解析】
试题分析:(1)由抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() ,求出c的值,进而求出抛物线方程;
,求出c的值,进而求出抛物线方程;
(2)如图1,由OE⊥PH,MF⊥PH,MH⊥OH,可证△OEH∽△HFM,可知HE,HF的比例关系,求出P点坐标;
(3)首先求出D点坐标,写出直线MD的表达式,由两直线平行,两三角形相似,可得NG∥MD,直线QG解析式.
试题解析:(1)∵M为抛物线![]() 的顶点,
的顶点,
∴M(2,c).
∴OH=2,MH=|c|.
∵a<0,且抛物线与x轴有交点,
∴c>0,
∴MH=c,
∵sin∠MOH=![]() ,
,
∴![]() .
.
∴OM=![]() c,
c,
∵OM2=OH2+MH2,
∴MH=c=4,
∴M(2,4),
∴抛物线的函数表达式为:y=-![]() (x-2)2+4.
(x-2)2+4.
(2)如图1,∵OE⊥PH,MF⊥PH,MH⊥OH,
∴∠EHO=∠FMH,∠OEH=∠HFM.
∴△OEH∽△HFM,
∴![]() ,
,
∵![]() ,
,
∴MF=HF,
∴∠OHP=∠FHM=45°,
∴OP=OH=2,
∴P(0,2).
如图2,同理可得,P(0,-2).
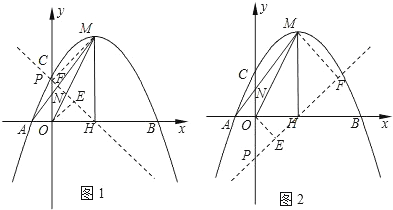
(3)∵A(-1,0),
∴D(1,0),
∵M(2,4),D(1,0),
∴直线MD解析式:y=4x-4,
∵ON∥MH,∴△AON∽△AHM,
∴![]() ,
,
∴AN=![]() ,ON=
,ON=![]() ,N(0,
,N(0,![]() ).
).
如图3,若△ANG∽△AMD,可得NG∥MD,
∴直线QG解析式:y=4x+![]() ,
,
如图4,若△ANG∽△ADM,可得![]()
∴AG=![]() ,
,
∴G(![]() ,0),
,0),
∴QG:y=-![]() ,
,
综上所述,符合条件的所有直线QG的解析式为:y=4x+![]() 或y=-
或y=-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
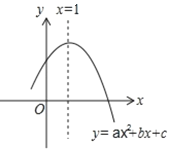
【题目】如图,二次函数![]() 的图象过点A(3,0),对称轴为直线
的图象过点A(3,0),对称轴为直线![]() ,给出以下结论:
,给出以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④若M(-3,
;④若M(-3,![]() )、N(6,
)、N(6,![]() )为函数图象上的两点,则
)为函数图象上的两点,则![]() ,其中正确的是____________.(只要填序号)
,其中正确的是____________.(只要填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学期末,某班评选一名优秀学生干部,下表是班长、学习委员和团支部书记的得分情况:

假设在评选优秀干部时,思想表现、学习成绩、工作能力这三方面的重要比为3 ∶3 ∶4 ,通过计算说明谁应当选为优秀学生干部。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形![]() 恰好被分割成3个边长为
恰好被分割成3个边长为![]() 的大正方形和4个边长为
的大正方形和4个边长为![]() 的小正方形,取1个大正方形和2个小正方形将两个小正方形放置在大正方形中(如图2所示).若图2中阴影都分的面积比四边形
的小正方形,取1个大正方形和2个小正方形将两个小正方形放置在大正方形中(如图2所示).若图2中阴影都分的面积比四边形![]() 的面积小80,则边长为
的面积小80,则边长为![]() 的正方形面积是________.
的正方形面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
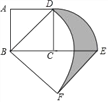
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一定是一元二次方程的有( )
(1)(a-1)x+bx+c=0(a,b,c是实数);(2)2x+![]() +3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)
+3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)![]() x-8=
x-8=![]() x
x
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年6月份,某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装荔枝和香蕉共5吨,且一辆甲种货车可装的荔枝重量(单位:吨)是其可装的香蕉重量的4倍,一辆乙种货车可装荔枝香蕉各2吨;
(1)一辆甲种货车可装载荔枝、香蕉各多少吨?
(2)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案?使运费最少?最少运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com