
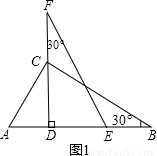
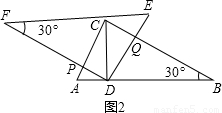
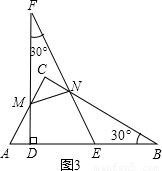
 x,那么PC=6-x.可表示出S△PCQ
x,那么PC=6-x.可表示出S△PCQ t,AB=12,那么BE=12-AD-DE=6-
t,AB=12,那么BE=12-AD-DE=6- t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN
t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN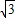
 x.
x.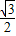 x2+3
x2+3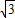 x
x t,BN=
t,BN=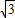 (6-
(6- t).
t). (6-t)×
(6-t)×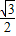 t=-
t=-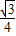 [(t-3)2-9]
[(t-3)2-9] x2+3
x2+3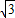 x=
x=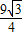
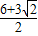 或
或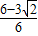
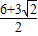 或AP=
或AP=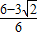 时,S△PCQ等于S△MCN的最大值.
时,S△PCQ等于S△MCN的最大值.

科目:初中数学 来源:2006年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年浙江省丽水市中考数学试卷(大纲卷)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年浙江省丽水市中考数学试卷(大纲卷)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2006年浙江省丽水市中考数学试卷(大纲卷)(解析版) 题型:选择题



查看答案和解析>>
科目:初中数学 来源:2006年浙江省丽水市中考数学试卷(大纲卷)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com