
 如图,在四边形ABCD中,∠ADC+∠BCD=270°,连结AC,点E、F、G分别是AB、CD、AC的中点,连结EF、FG,分别将AD、BC作为边长,向外作正方形.若这两个正方形的面积和为12cm2,则EF的长度为$\sqrt{3}$cm.
如图,在四边形ABCD中,∠ADC+∠BCD=270°,连结AC,点E、F、G分别是AB、CD、AC的中点,连结EF、FG,分别将AD、BC作为边长,向外作正方形.若这两个正方形的面积和为12cm2,则EF的长度为$\sqrt{3}$cm. 分析 如图,连接EG,延长AD、BC交于点M.首先证明AM⊥BM,再证明EG⊥GF,根据EF=$\sqrt{E{G}^{2}+G{F}^{2}}$以及EG2+GF2=$\frac{1}{4}$(AD2+BC2)计算即可解决问题.
解答 解:如图,连接EG,延长AD、BC交于点M.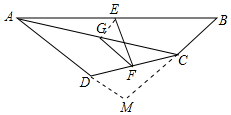
∵∠ADC+∠BCD=270°,
∴∠MAB+∠B=360°-270°=90°,
∴∠M=90°,
∴AM⊥BM,
∵AE=EB,AG=GC,
∴EG∥BM,EG=$\frac{1}{2}$BC,
∵AG=CG,CF=DF,
∴GF∥AM,GF=$\frac{1}{2}$AD,
∴EG⊥GF,
∴△EGF是直角三角形,
∵AD2+BC2=12,
∴EG2+GF2=$\frac{1}{4}$(AD2+BC2)=3,
∴EF=$\sqrt{E{G}^{2}+G{F}^{2}}$=$\sqrt{3}$cm,
故答案为$\sqrt{3}$cm.
点评 本题考查三角形中位线定理、正方形的性质、勾股定理、四边形内角和定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,解题的突破点是发现△EGF是直角三角形,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
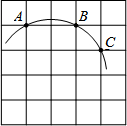 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,4),点C的坐标是(1,3),那么这条圆弧所在圆的圆心坐标是(-1,2).
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,4),点C的坐标是(1,3),那么这条圆弧所在圆的圆心坐标是(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校计划修建一个长方形花坛,要求花坛的长与宽的比为2:1,如图所示花坛中间为花卉种植区域,花卉种植区域前侧留有2米宽的空地,其它三侧各保留1米宽的通道,如果要求花卉种植区域的面积是55平方米,那么整个花坛的长与宽应为多少米?
某校计划修建一个长方形花坛,要求花坛的长与宽的比为2:1,如图所示花坛中间为花卉种植区域,花卉种植区域前侧留有2米宽的空地,其它三侧各保留1米宽的通道,如果要求花卉种植区域的面积是55平方米,那么整个花坛的长与宽应为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com