
【题目】已知关于x的一元二次方程![]() .(其中m为实数)
.(其中m为实数)
(1)若此方程的一个非零实数根为k,
① 当k = m时,求m的值;
② 若记![]() 为y,求y与m的关系式;
为y,求y与m的关系式;
(2)当![]() <m<2时,判断此方程的实数根的个数并说明理由
<m<2时,判断此方程的实数根的个数并说明理由
【答案】(1)
①1
②![]()
(2)当![]() <m<2时,此方程有两个不相等的实数根
<m<2时,此方程有两个不相等的实数根
【解析】解:(1)∵ k为![]() 的实数根,
的实数根,
∴![]() .※ …………………………………………1分
.※ …………………………………………1分
① 当k = m时,
∵ k为非零实数根,
∴ m ≠ 0,方程※两边都除以m,得![]() .
.
整理,得![]() .
.
解得![]() ,
, ![]() . ………………………………………………………2分
. ………………………………………………………2分
∵![]() 是关于x的一元二次方程,
是关于x的一元二次方程,
∴ m ≠ 2.
∴ m=" 1." ……………………………………………………………………3分
(阅卷说明:写对m= 1,但多出其他错误答案扣1分)
② ∵ k为原方程的非零实数根,
∴ 将方程※两边都除以k,得![]() .…………………4分
.…………………4分
整理,得![]() .
.
∴![]() .……………………………………………5分
.……………………………………………5分
(2)解法一: ![]() .………6分
.………6分
当![]() <m<2时,m>0,
<m<2时,m>0, ![]() <0.
<0.
∴![]() >0,
>0, ![]() >1>0,Δ>0.
>1>0,Δ>0.
∴ 当![]() <m<2时,此方程有两个不相等的实数根. ……………7分
<m<2时,此方程有两个不相等的实数根. ……………7分
解法二:直接分析![]() <m<2时,函数
<m<2时,函数![]() 的图象,
的图象,
∵ 该函数的图象为抛物线,开口向下,与y轴正半轴相交,
∴ 该抛物线必与x轴有两个不同交点. …………………………6分
∴ 当![]() <m<2时,此方程有两个不相等的实数根. ……………7分
<m<2时,此方程有两个不相等的实数根. ……………7分
解法三: ![]() .…………6分
.…………6分
结合![]() 关于m的图象可知,(如图6)
关于m的图象可知,(如图6)
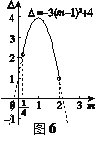
当![]() <m≤1时,
<m≤1时, ![]() <
<![]() ≤4;
≤4;
当1<m<2时,1<![]() <4.
<4.
∴ 当![]() <m<2时,
<m<2时, ![]() >0.
>0.
∴ 当![]() <m<2时,此方程有两个不相等的实数根.…7分
<m<2时,此方程有两个不相等的实数根.…7分


科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.点P(3,﹣5)到x轴的距离为﹣5
B.在平面直角坐标系内,(﹣1,2)和(2,﹣1)表示同一个点
C.若x=0,则点P(x,y)在x轴上
D.在平面直角坐标系中,有且只有一个点既在x轴上,又在y轴上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔25元,而按原定价的九折出售,每件将赚20元,则这种商品的原定价是( )
A.200元B.300元C.320元D.360元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作三角形的类型:
尺 规 作 图 | 类型 | 依据 |
已知两边及其夹角作三角形 | __________ | |
已知两角一边作三角形 | __________(或 | |
已知三边作三角形 | __________ |
【答案】 SAS ASA SSS
【解析】试题解析:已知两边及其夹角作三角形,其依据是:SAS.
已知两角一边作三角形,其依据是:ASA(或![]() ).
).
已知三边作三角形, 其依据是: ![]()
故答案为: ![]()
点睛:判定三角形全等的方法有: ![]()
【题型】填空题
【结束】
11
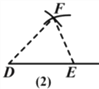
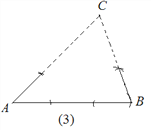
【题目】如图,根据图中作图痕迹,可以得出作三角形的依据分别是:
(1)__________;
(2)___________;
(3)__________.(图中虚线表示最后作出的线段)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a=![]() ;③ac=b﹣1;④
;③ac=b﹣1;④![]() >0
>0
其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使![]() ,求点P的坐标;
,求点P的坐标;
(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果).
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com