
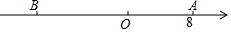 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.
如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.分析 (1)根据已知可得B点表示的数为8-20;点P表示的数为8-5t;
(2)设t秒时P、Q之间的距离恰好等于2.分两种情况:①点P、Q相遇之前,②点P、Q相遇之后,列出方程求解即可;
(3)设点P运动x秒时,P、Q之间的距离恰好等于2.分两种情况:①点P、Q相遇之前,②点P、Q相遇之后,列出方程求解即可;
(4)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
解答 解:(1)数轴上点B表示的数为8-20=-12;点P表示的数为8-5t;
(2)若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=20,解得t=2.25;
②点P、Q相遇之后,
由题意得3t-2+5t=20,解得t=2.75.
答:若点P、Q同时出发,2.25或2.75秒时P、Q之间的距离恰好等于2;
(3)设点P运动x秒时,P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
则5x-3x=20-2,
解得:x=9;
②点P、Q相遇之后,
则5x-3x=20+2
解得:x=11.
答:若点P、Q同时出发,9或11秒时P、Q之间的距离恰好又等于2;
(4)线段MN的长度不发生变化,都等于10;理由如下:
①当点P在点A、B两点之间运动时:
MN=MP+NP=$\frac{1}{2}$AP+$\frac{1}{2}$BP=$\frac{1}{2}$(AP+BP)=$\frac{1}{2}$AB=$\frac{1}{2}$×20=10,
②当点P运动到点B的左侧时:
MN=MP-NP=$\frac{1}{2}$AP-$\frac{1}{2}$BP=$\frac{1}{2}$(AP-BP)=$\frac{1}{2}$AB=10,
则线段MN的长度不发生变化,其值为10.
故答案为:-12;8-5t.
点评 本题考查了数轴、一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
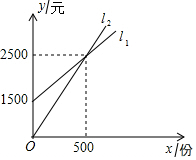 某公司要印制产品宣传材料,l1反映了甲印刷厂的收费y1(元)与印制数量x(份)间的关系,l2反映了乙印刷厂的收费y2(元)与印制数量x(份)间的关系.
某公司要印制产品宣传材料,l1反映了甲印刷厂的收费y1(元)与印制数量x(份)间的关系,l2反映了乙印刷厂的收费y2(元)与印制数量x(份)间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等边△ABC的边长为2,E,F,G分别在边AB,BC,CA上,且△EFG也是等边三角形.
如图,已知等边△ABC的边长为2,E,F,G分别在边AB,BC,CA上,且△EFG也是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
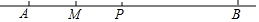 如图,线段AB=24,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
如图,线段AB=24,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com