
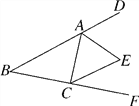
【题目】如图,在△ABC中,∠B=40°,△ABC的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
【答案】70°
【解析】试题分析:先根据三角形内角和定理计算出∠BAC+∠BCA=180°-∠B=140°,则利邻补角定义计算出∠DAC+∠FCA=180°-∠BAC+180°-∠BCA=220°,再根据角平分线定义得到∠EAC=![]() ∠DAC,∠ECA=
∠DAC,∠ECA=![]() ∠FCA,所以∠EAC+∠ECA=
∠FCA,所以∠EAC+∠ECA=![]() (∠DAC+∠FCA)=110°,然后再利用三角形内角和计算∠AEC的度数.
(∠DAC+∠FCA)=110°,然后再利用三角形内角和计算∠AEC的度数.
试题解析:在△ABC中,∵∠B=40°,
∴∠BAC+∠BCA=180°-40°=140°,
∵∠DAC+∠BAC=180°,∠ACF+∠ACB=180°,
∴∠DAC+∠ACF=360°-140°=220°,
∵AE平分∠DAC,CE平分∠ACF,
∴∠EAC+∠ECA=![]() (∠DAC+∠ACF)=110°,
(∠DAC+∠ACF)=110°,
∴∠AEC=180°-110°=70°.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.

⑴ 求证:AB=AC.
⑵ 若BD=11,DE=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交与
轴分别交与![]() 、
、![]() 两点,
两点,![]() .
.
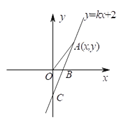
(![]() )写出
)写出![]() 点的坐标和
点的坐标和![]() 的值.
的值.
(![]() )若点
)若点![]() 是第一象限内的直线
是第一象限内的直线![]() 上的一个动点,当点
上的一个动点,当点![]() 运动过程中,试求出
运动过程中,试求出![]() 的面积
的面积![]() 与
与![]() 的函数关系式.
的函数关系式.
(![]() )在(
)在(![]() )的条件下:
)的条件下:
①当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() .
.
②在①成立的情况下,![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 是等腰三角形.若存在,请写出满足条件的所有
是等腰三角形.若存在,请写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)试问在x轴上是否存在一点P,使PC-PB最大,若存在,求出PC-PB的最大值及P点坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
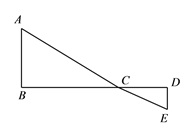
【题目】如图, ![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 、
、![]() 作
作![]() ,
, ![]() ,连接
,连接![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)请问点![]() 在什么位置时,
在什么位置时, ![]() 的值最小,求出这个最小值;
的值最小,求出这个最小值;
(3)根据(2)中的规律和结论,构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
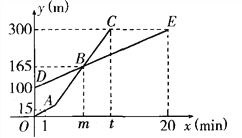
【题目】小强和爸爸上山游玩,两人距地面的高度y(m)与小强登山时间x(min)之间的函数图像分别如图中折线OAC(小强)和线段DE(爸爸)所示,根据函数图像进行以下探究:
(1)爸爸登山的速度是每分钟_______m;
(2)请解释图中点B的实际意义;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(4)求m的值;
(5)若小强提速后,他登山的速度是爸爸速度的3倍,试问小强登山多长时间时开始提速?此时小强距地面的高度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华商场将进价为40元的衬衫按50元售出时,每月能卖出500件,经市场调查,这种衬衫每件涨价4元,其销售量就减少40件.如果商场计划每月赚得8000元利润,那么售价应定为多少?这时每月应进多少件衬衫?
查看答案和解析>>
科目:初中数学 来源: 题型:
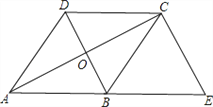
【题目】如图,已知菱形ABCD的对角线AC 、BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
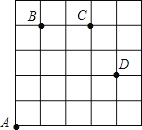
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出依次行走停点E、F、M、N的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com