
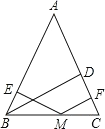
【题目】大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可 以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高为h,M 是底边BC上的任意一点,M 到腰AB、AC 的距离分别为 h1、h2 .
(1)请你结合图形来证明: h1+h2=h;
(2)当点M在BC延长线上时,h1、h2、h 之间又有什么样的结论.请你画出图形,并直
接写出结论不必证明;
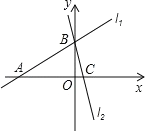
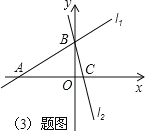
(3)利用以上结论解答,如图在平面直角坐标系中有两条直线l1:y=x+3,l2:y=-3x+3
若 l2上的一点M 到l1的距离是![]() ,求点 M 的坐标.
,求点 M 的坐标.
【答案】(1)证明见解析;(2)h1﹣h2=h;(3)点 M 的坐标为 M(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)根据S△ABC=S△ABM+S△AMC即可求出答案;
(2)h1-h2=h;
(3)先求得△ABC为等腰三角形,再根据(1)(2)的结果分①当点M在BC边上时,②当点M在CB延长线上时,求得M的坐标.③当点M在BC的延长线上时,h1=![]() <h,不存在.
<h,不存在.
(1)证明:连接 AM,
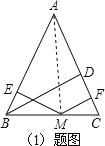
由题意得 h1=ME,h2=MF,h=BD,
∵S△ABC=S△ABM+S△AMC,
S△ABM=![]() ×AB×ME=
×AB×ME=![]() ×AB×h1,
×AB×h1,
S△AMC=![]() ×AC×MF=
×AC×MF=![]() ×AC×h2,
×AC×h2,
又∵S△ABC=![]() ×AC×BD=
×AC×BD=![]() ×AC×h,AB=AC,
×AC×h,AB=AC,
∴![]() ×AC×h=
×AC×h=![]() ×AB×h1+
×AB×h1+![]() ×AC×h2,
×AC×h2,
∴h1+h2=h.
(2)如图所示:
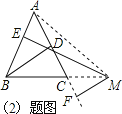
h1﹣h2=h.
(3)解:在 y=![]() x+3 中,令 x=0 得 y=3;令 y=0 得 x=﹣4,所以 A(﹣4,0),B(0,3)
x+3 中,令 x=0 得 y=3;令 y=0 得 x=﹣4,所以 A(﹣4,0),B(0,3)
同理求得 C(1,0).
AB=![]() =5,AC=5,所以 AB=AC,
=5,AC=5,所以 AB=AC,
即△ABC 为等腰三角形.
(ⅰ)当点 M 在 BC 边上时,由 h1+h2=h 得:![]() +My=OB,My=3﹣
+My=OB,My=3﹣![]() =
=![]() , 把它代入y=﹣3x+3 中求得:Mx=
, 把它代入y=﹣3x+3 中求得:Mx=![]() ,所以此时 M(
,所以此时 M(![]() ,
,![]() )
)
(ⅱ)当点 M 在 CB 延长线上时,由 h1﹣h2=h 得:My﹣![]() =OB,My=3+
=OB,My=3+![]() =
=![]() ,
,
把它代入 y=﹣3x+3 中求得:Mx=﹣![]() , 所以此时 M(﹣
, 所以此时 M(﹣![]() ,
,![]() ).
).
综合(ⅰ)、(ⅱ)知:点 M 的坐标为 M(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E. 
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块长为a米,宽为b米的矩形空地建成一个矩形花园,要求在花园中修两条入口宽均为x米的小道,其中一条小道两边分别经过矩形一组对角顶点,剩余的地方种植花草,现有从左至右三种设计方案如图所示,种植花草的面积分别为S1,S2和S3,则它们的大小关系为( )

A. S3<S1<S2 B. S1<S2<S3 C. S2<S1<S3 D. S1=S2=S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
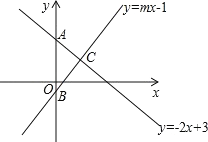
【题目】如图,直线y1=-2x+3和直线y2=mx-3分别交y轴于点A、B ,两直线交于点C(1,n).
(1)求 m、n 的值;
(2)求△ABC的面积;
(3)请根据图象直接写出:当 y1<y2时,自变量 x 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG. 
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com