
”¾ĢāÄæ”æijŹ³Ę·¼Ó¹¤³§ŠčŅŖŅ»ÅśŹ³Ę·°ü×°ŗŠ£¬¹©Ó¦ÕāÖÖ°ü×°ŗŠÓŠĮ½ÖÖ·½°øæɹ©Ń”Ōń£ŗ
·½°øŅ»£ŗ“Ó°ü×°ŗŠ¼Ó¹¤³§Ö±½Ó¹ŗĀņ£¬¹ŗĀņĖłŠčµÄ·Ńy1Óė°ü×°ŗŠŹżxĀś×ćČēĶ¼1ĖłŹ¾µÄŗÆŹż¹ŲĻµ£®
·½°ø¶ž£ŗ×āĮŽ»śĘ÷×Ō¼ŗ¼Ó¹¤£¬ĖłŠč·ŃÓĆy2£Ø°üĄØ×āĮŽ»śĘ÷µÄ·ŃÓĆŗĶÉś²ś°ü×°ŗŠµÄ·ŃÓĆ£©Óė°ü×°ŗŠŹżxĀś×ćČēĶ¼2ĖłŹ¾µÄŗÆŹż¹ŲĻµ£®øł¾ŻĶ¼Ļó»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©·½°øŅ»ÖŠĆæøö°ü×°ŗŠµÄ¼ŪøńŹĒ¶ąÉŁŌŖ£æ
£Ø2£©·½°ø¶žÖŠ×āĮŽ»śĘ÷µÄ·ŃÓĆŹĒ¶ąÉŁŌŖ£æÉś²śŅ»øö°ü×°ŗŠµÄ·ŃÓĆŹĒ¶ąÉŁŌŖ£æ
£Ø3£©Ēė·Ö±šĒó³öy1”¢y2ÓėxµÄŗÆŹż¹ŲĻµŹ½£®
£Ø4£©Čē¹ūÄćŹĒ¾ö²ßÕߣ¬ÄćČĻĪŖÓ¦øĆŃ”ŌńÄÄÖÖ·½°øøüŹ”Ē®£æ²¢ĖµĆ÷ĄķÓÉ

”¾“š°ø”æ(1)”¢5ŌŖ£»(2)”¢20000ŌŖ£»2.5ŌŖ£»(3)”¢y1=5x£»y2=2.5x+20000£»(4)”¢µ±x=8000Ź±£¬Į½ÖÖ·½°øĶ¬ŃłŹ”Ē®£»µ±x£¼8000Ź±£¬Ń”Ōń·½°øŅ»£»µ±x£¾8000Ź±£¬Ń”Ōń·½°ø¶ž.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ(1)”¢øł¾ŻĶ¼Ņ»µĆ³ö“š°ø£»(2)”¢øł¾ŻĶ¼¶žµĆ³ö×āĮŽ»śĘ÷µÄ·ŃÓĆŗĶŗŠ×ӵĵ„¼Ū£»(3)”¢ĄūÓĆ“ż¶ØĻµŹż·Ø·Ö±šĒó³öĮ½øöŗÆŹżµÄ½āĪöŹ½£»(4)”¢Ź×ĻČĒó³öĮ½øöĻąµČŹ±xµÄÖµ£¬Č»ŗóµĆ³ö“š°ø.
ŹŌĢā½āĪö£ŗ(1)”¢500”Ā100=5£¬ ”ą·½°øŅ»µÄŗŠ×Óµ„¼ŪĪŖ5ŌŖ£»
(2)”¢øł¾ŻŗÆŹżµÄĶ¼ĻóæÉŅŌÖŖµĄ×āĮŽ»śĘ÷µÄ·ŃÓĆĪŖ20000ŌŖ£¬
ŗŠ×ӵĵ„¼ŪĪŖ£Ø30000©20000£©”Ā4000=2.5£¬ ¹ŹŗŠ×ӵĵ„¼ŪĪŖ2.5ŌŖ£»
(3)”¢ÉčĶ¼ĻóŅ»µÄŗÆŹż½āĪöŹ½ĪŖ£ŗy1=k1x£¬ ÓÉĶ¼ĻóÖŖŗÆŹż¾¹żµć£Ø100£¬500£©£¬ ”ą500=100k1£¬
½āµĆk1=5£¬ ”ąŗÆŹżµÄ½āĪöŹ½ĪŖy1=5x£»
ÉčĶ¼Ļ󶞵ÄŗÆŹż¹ŲĻµŹ½ĪŖy2=k2x+b
ÓÉĶ¼ĻóÖŖµĄŗÆŹżµÄĶ¼Ļó¾¹żµć£Ø0£¬20000£©ŗĶ£Ø4000£¬30000£©”ą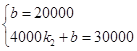 £¬
£¬
½āµĆ£ŗ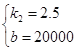 £¬ ”ąŗÆŹżµÄ½āĪöŹ½ĪŖy2=2.5x+20000£»
£¬ ”ąŗÆŹżµÄ½āĪöŹ½ĪŖy2=2.5x+20000£»
(4)”¢Įī5x=2.5x+20000£¬ ½āµĆx=8000£¬
”ąµ±x=8000Ź±£¬Į½ÖÖ·½°øĶ¬ŃłŹ”Ē®£»µ±x£¼8000Ź±£¬Ń”Ōń·½°øŅ»£»µ±x£¾8000Ź±£¬Ń”Ōń·½°ø¶ž£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ÓŠ5ÕÅŠ“×Ų»Ķ¬ŹżµÄæØʬ£¬ĒėÄć·Ö±š°“ŅŖĒó³é³öæØʬ£¬Š“³ö·ūŗĻŅŖĒóµÄĖćŹ½£ŗ
![]()
(1)“ÓÖŠČ”³ö2ÕÅæØʬ£¬Ź¹Õā2ÕÅæØʬÉĻµÄŹżµÄ³Ė»ż×ī“ó£»
(2)“ÓÖŠČ”³ö2ÕÅæØʬ£¬Ź¹Õā2ÕÅæØʬÉĻµÄŹżĻą³żµÄÉĢ×īŠ”£»
(3)“ÓÖŠČ”³ö2ÕÅæØʬ£¬Ź¹Õā2ÕÅæØʬÉĻµÄŹżĶعżÓŠĄķŹżµÄŌĖĖćŗóµĆµ½µÄ½į¹ū×ī“ó£»
(4)“ÓÖŠČ”³ö4ÕÅæØʬ£¬Ź¹Õā4ÕÅæØʬĶعżÓŠĄķŹżµÄŌĖĖćŗóµĆµ½µÄ½į¹ūĪŖ24.(Š“³öŅ»ÖÖ¼“æÉ)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪåŌĀ³õ£¬ĪŅŹŠ¶ąµŲŌāÓöĮĖ³ÖŠųĒæ½µÓźµÄ¶ńĮÓĢģĘų£¬Ōģ³É²æ·ÖµŲĒų³öĻÖŃĻÖŲŗéĄŌŌÖŗ¦£¬Ä³°®ŠÄ×éÖƽō¼±³ļ¼ÆĮĖ²æ·Ö׏½š£¬¼Ę»®¹ŗĀņ¼×”¢ŅŅĮ½ÖÖ¾ČŌÖĪļĘ·¹²2000¼žĖĶĶłŌÖĒų£¬ŅŃÖŖĆ漞¼×ÖÖĪļĘ·µÄ¼Ūøń±ČĆ漞ŅŅÖÖĪļĘ·µÄ¼Ūøń¹ó10ŌŖ£¬ÓĆ350ŌŖ¹ŗĀņ¼×ÖÖĪļĘ·µÄ¼žŹżĒ”ŗĆÓėÓĆ300ŌŖ¹ŗĀņŅŅÖÖĪļĘ·µÄ¼žŹżĻąĶ¬
£Ø1£©Ēó¼×”¢ŅŅĮ½ÖÖ¾ČŌÖĪļĘ·Ć漞µÄ¼Ūøńø÷ŹĒ¶ąÉŁŌŖ£æ
£Ø2£©¾µ÷²é£¬ŌÖĒų¶ŌŅŅÖÖĪļĘ·¼žŹżµÄŠčĒóĮæŹĒ¼×ÖÖĪļĘ·¼žŹżµÄ3±¶£¬ČōøĆ°®ŠÄ×éÖÆ°“ÕÕ“ĖŠčĒóµÄ±ČĄż¹ŗĀņÕā2000¼žĪļĘ·£¬Šč³ļ¼Æ׏½š¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ė®°ÓµÄŗį¶ĻĆęŹĒĢŻŠĪ£¬±³Ė®ĘĀABµÄĘĀ½Ē”ĻBAD=60”ć£¬ĘĀ³¤AB=20 ![]() m£¬ĪŖ¼ÓĒæĖ®°ÓĒæ¶Č£¬½µ°Óµ×“ÓA“¦ŗóĖ®Ę½ŃÓÉģµ½F“¦£¬Ź¹ŠĀµÄ±³Ė®ĘĀ½Ē”ĻF=45”ć£¬ĒóAFµÄ³¤¶Č£Ø½į¹ū¾«Č·µ½1Ć×£¬²Īæ¼Źż¾Ż£ŗ
m£¬ĪŖ¼ÓĒæĖ®°ÓĒæ¶Č£¬½µ°Óµ×“ÓA“¦ŗóĖ®Ę½ŃÓÉģµ½F“¦£¬Ź¹ŠĀµÄ±³Ė®ĘĀ½Ē”ĻF=45”ć£¬ĒóAFµÄ³¤¶Č£Ø½į¹ū¾«Č·µ½1Ć×£¬²Īæ¼Źż¾Ż£ŗ ![]() 1.414£¬
1.414£¬ ![]() ”Ö1.732£©£®
”Ö1.732£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
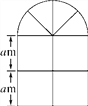
”¾ĢāÄæ”æ£Ø12·Ö£©ČēĶ¼ŹĒijÖÖ“°»§µÄŠĪד£¬ĘäÉĻ²æŹĒ°ėŌ²ŠĪ£¬ĻĀ²æŹĒ±ß³¤ĻąĶ¬µÄĖÄøöŠ”Õż·½ŠĪ£¬ŅŃÖŖĻĀ²æµÄŠ”Õż·½ŠĪµÄ±ß³¤ĪŖam£¬¼ĘĖć£ŗ
£Ø1£©“°»§µÄĆ껿£»
£Ø2£©“°æņµÄ×ܳ¤£»
£Ø3£©Čōa£½1£¬“°»§ÉĻ°²×°µÄŹĒ²£Į§£¬²£Į§ĆæĘ½·½Ć×25ŌŖ£¬“°æņĆæĆ×20ŌŖ£¬“°æņµÄŗń¶Č²»¼Ę£¬ĒóÖĘ×÷ÕāÖÖ“°»§ŠčŅŖµÄ·ŃÓĆŹĒ¶ąÉŁŌŖ£Ø¦ŠČ”3.14£¬½į¹ū±£ĮōÕūŹż£©.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā·½³Ģ
£Ø1£©x2£½49
£Ø2£©3x2£7x£½0
£Ø3£©![]() £ØÖ±½ÓæŖĘ½·½·Ø£©
£ØÖ±½ÓæŖĘ½·½·Ø£©
£Ø4£©![]() £ØÓĆÅä·½·Ø£©
£ØÓĆÅä·½·Ø£©
£Ø5£©![]() £ØŅņŹ½·Ö½ā·Ø£©
£ØŅņŹ½·Ö½ā·Ø£©
£Ø6£©![]()
£Ø7£©£Øx£2£©£Øx£5£©=£2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½āĻĀĮŠ·½³Ģ
£Ø1£©x2+6x©1=0
£Ø2£©£Ø2x+3£©2©25=0£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬AEŹĒ”÷ABCµÄ½ĒĘ½·ÖĻߣ»EDĘ½·Ö”ĻAEB£¬½»ABÓŚµćD£»”ĻCAE”ĻB£®

£Ø1£©Ēó”ĻBµÄ¶ČŹż£®
£Ø2£©Čē¹ūAC=3cm£¬ĒóABµÄ³¤¶Č£®
£Ø3£©²ĀĻė£ŗEDÓėABµÄĪ»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»Ī»ĄŗĒņŌĖ¶ÆŌ±ĢųĘšĶ¶Ąŗ£¬ĒņŃŲÅ×ĪļĻßy=© ![]() x2+3.5ŌĖŠŠ£¬Č»ŗó×¼Č·ĀäČėĄŗæņÄŚ£®ŅŃÖŖĄŗæņµÄÖŠŠÄĄėµŲĆęµÄ¾ąĄėĪŖ3.05Ć×£®
x2+3.5ŌĖŠŠ£¬Č»ŗó×¼Č·ĀäČėĄŗæņÄŚ£®ŅŃÖŖĄŗæņµÄÖŠŠÄĄėµŲĆęµÄ¾ąĄėĪŖ3.05Ć×£® 
£Ø1£©ĒņŌŚæÕÖŠŌĖŠŠµÄ×ī“óø߶ČĪŖ¶ąÉŁĆ×£æ
£Ø2£©Čē¹ūøĆŌĖ¶ÆŌ±ĢųĶ¶Ź±£¬Ēņ³öŹÖĄėµŲĆęµÄø߶ČĪŖ2.25Ć×£¬ĒėĪŹĖū¾ąĄėĄŗæņÖŠŠÄµÄĖ®Ę½¾ąĄėŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com