
【题目】如图,分别以△ABC的边AB、AC为一边,向外作正方形ABEF和正方形AGHC像这样的两个正方形称为△ABC的“依伴正方形”
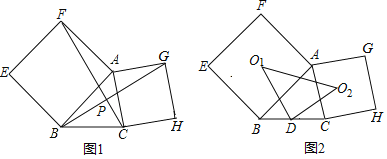
(1)如图1,连接BG,CF相交于点P,求证:BG=CF且BG⊥CF;
(2)如图2,点D是BC的中点,两个依伴正方形的中心分别为O1,O2连结O1D,O2D,O1O2:,判断△DO1O2的形状并说明由;
(3)如图2,若AB=6,AC=![]() ,∠BAC=60°,求O1O2的长.
,∠BAC=60°,求O1O2的长.
【答案】(1)见解析;(2)△DO1O2的形状是等腰直角三角形;理由见解析;(3)![]()
【解析】
(1)由SAS证明△FAC≌△BAG,得出BG=CF,∠AFC=∠ABG,设AB与FC的交点为Q,则∠FPG=∠ABG+∠BQP=∠AFC+∠AQF=90°,即可得出结论.
(2)连接FC、BG、FB、GC,证得O1D是△BCF的中位线,得出O1D=![]() FC,O1D∥FC,同理可得O2D是△CBG的中位线,得出O2D=
FC,O1D∥FC,同理可得O2D是△CBG的中位线,得出O2D=![]() BG,O2D∥BG,推出O1D=O2D,O1D⊥O2D,即可得出结论.
BG,O2D∥BG,推出O1D=O2D,O1D⊥O2D,即可得出结论.
(3)作FM⊥CA交其延长线于点M,证得∠FAM=180°﹣∠FAB﹣∠BAC=30°,则MF=![]() AF=3,AM=3
AF=3,AM=3![]() ,MC=MA+AC=6
,MC=MA+AC=6![]() ,FC=
,FC=![]() ,推出O1D=
,推出O1D=![]() FC,O1O2=
FC,O1O2=![]() O1D即可得出结论.
O1D即可得出结论.
(1)证明:∵四边形ABEF和四边形AGHC是正方形,
∴AF=AB,AC=AG,∠FAB=∠CAG=90°,
∴∠FAB+∠BAC=∠CAG+∠BAC,
即∠FAC=∠BAG,
在△FAC和△BAG中, ,
,
∴△FAC≌△BAG(SAS),
∴BG=CF,∠AFC=∠ABG,
∵∠AQF=∠BQP,
∴∠FPG=∠ABG+∠BQP=∠AFC+∠AQF=90°,
∴BG⊥CF;
(2)解:△DO1O2的形状是等腰直角三角形;理由如下:
连接FC、BG、FB、GC,如图2所示:
由(1)得:FC=BG,FC⊥BG,
∵O1是正方形ABEF的中心,
∴O1是BF的中点,
∵D是BC的中点,
∴O1D是△BCF的中位线,
∴O1D=![]() FC,O1D∥FC,
FC,O1D∥FC,
同理O2D是△CBG的中位线,
∴O2D=![]() BG,O2D∥BG,
BG,O2D∥BG,
∴O1D=O2D,O1D⊥O2D,
∴△DO1O2为等腰直角三角形;
(3)解:作FM⊥CA交其延长线于点M,如图3所示:
∵四边形ABEF是正方形,
∴AB=AF=6,∠FAB=90°,
∵∠BAC=60°,
∴∠FAM=180°﹣∠FAB﹣∠BAC=30°,
∴MF=![]() AF=3,AM=tan60°FM=
AF=3,AM=tan60°FM=![]() FM=3
FM=3![]() ,
,
∴MC=MA+AC=6![]() ,
,
∴FC=![]() ,
,
∴O1D=![]() FC=
FC=![]() ,
,
∴O1O2=![]() O1D=
O1D=![]() .
.



 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
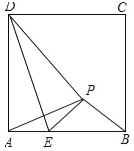
【题目】如图,正方形ABCD中,AD=![]() +2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房![]() 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天![]() 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加![]() 元,就会减少
元,就会减少![]() 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 如果某天宾馆客房收入
如果某天宾馆客房收入![]() 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A与原点O重合,顶点B在直线l上,将正方形沿射线OB方向无滑动地翻滚.若直线![]() ,正方形边长为2
,正方形边长为2![]()
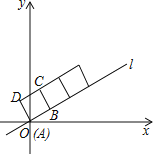
(1)翻滚后点A第一次落在直线l上的坐标是_____;
(2)当正方形翻滚2002次点A对应点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
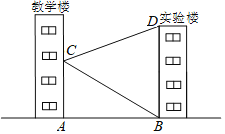
【题目】如图,学校教学楼对面是一幢实验楼,小朱在教学楼的窗口C测得实验楼顶部D的仰角为20°,实验楼底部B的俯角为30°,量得教学楼与实验楼之间的距离AB=30m.求实验楼的高BD.(结果精确到1m.参考数据tan20°≈0.36,sin20°≈0.34,cos20°≈0.94,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为![]() 的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程
的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解.利用上述材料给你的启示,解下列方程;
的解.利用上述材料给你的启示,解下列方程;
(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鱼塘中养了某种鱼5000条,为了估计该鱼塘中该种鱼的总质量,从鱼塘中捕捞了3次,取得的数据如下:
数量/条 | 平均每条鱼的质量/kg | |
第1次捕捞 | 20 | 1.6 |
第2次捕捞 | 15 | 2.0 |
第3次捕捞 | 15 | 1.8 |
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为14元,求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数关系,并估计自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,顶点为
两点,顶点为![]() ,设点
,设点![]() 是
是![]() 轴的正半轴上一点,将抛物线
轴的正半轴上一点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.

![]() 求抛物线
求抛物线![]() 的函数表达式:
的函数表达式:
![]() 若抛物线
若抛物线![]() 与抛物线
与抛物线![]() 在
在![]() 轴的右侧有两个不同的公共点,求
轴的右侧有两个不同的公共点,求![]() 的取值范围.
的取值范围.
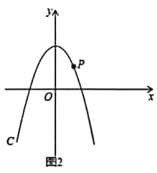
![]() 如图2,
如图2,![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,它到两坐标轴的距离相等,点
上一点,它到两坐标轴的距离相等,点![]() 在抛物线
在抛物线![]() 上的对应点
上的对应点![]() ,设
,设![]() 是
是![]() 上的动点,
上的动点,![]() 是
是![]() 上的动点,试探究四边形
上的动点,试探究四边形![]() 能否成为正方形?若能,求出
能否成为正方形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com