
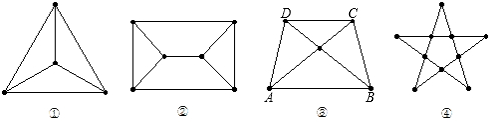
| 图 | 顶点数 | 边数 | 区域数 |
| ① | |||
| ② | |||
| ③ | 5 | 8 | 4 |
| ④ |
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
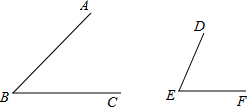 (2012•佛山)比较两个角的大小,有以下两种方法(规则)
(2012•佛山)比较两个角的大小,有以下两种方法(规则)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届江苏省南京市白下区中考二模数学试卷(带解析) 题型:解答题
(1)如图①,P为△ABC的边AB上一点(P不与点A、点B重合),连接PC,如果△CBP∽△ABC,那么就称P为△ABC的边AB上的相似点.
画法初探
①如图②,在△ABC中,∠ACB>90°,画出△ABC的边AB上的相似点P(画图工具不限,保留画图痕迹或有必要的说明);
辩证思考
②是不是所有的三角形都存在它的边上的相似点?如果是,请说明理由;如果不是,请找出一个不存在边上相似点的三角形;
特例分析
③已知P为△ABC的边AB上的相似点,连接PC,若△ACP∽△ABC,则△ABC的形状是 ;
④如图③,在△ABC中,AB=AC,∠A=36°,P是边AB上的相似点,求的值.
(2)在矩形ABCD中,AB=a,BC=b(a≥b).P是AB上的点(P不与点A、点B重合),作PQ⊥CD,垂足为Q.如果矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.
①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
你的解答是: (只需描述PQ的画法,不需在图上画出PQ).
②请继续类比(1)中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究,要求每个栏目提出一个问题并解决.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com