
����Ŀ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮����ijУ�ٰ��������й�ʫ�ʱ�������ȫУʦ��ͬʱĬд50��ʫ��ÿ��ȷĬд��һ��ʫ��2�֣������600��ѧ������������ӽ��������600��ѧ���������ȡ40��ѧ�����гɼ����������ݱ����ɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ������ͼ��
��� | �ɼ�x���֣� | Ƶ���������� |
��1�� | 60��x��68 | 4 |
��2�� | 68��x��76 | 8 |
��3�� | 76��x��84 | 12 |
��4�� | 84��x��92 | a |
��5�� | 92��x��100 | 10 |
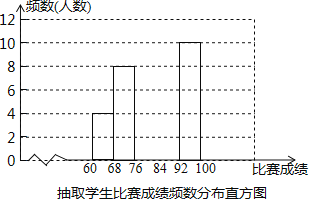
��3��12��ѧ���ı����ɼ�Ϊ��76��76��78��78��78��78��78��78��80��80��80��82��������������Ϣ������и��⣺
��1����գ�a���� ������ȡ��40��ѧ�������ɼ�����λ������ ��
��2���뽫Ƶ���ֲ�ֱ��ͼ��������
��3���������ɼ�������84�ֵ�Ϊ���㣬���ƽ��������ѧ�����ж�����ѧ���ı����ɼ�Ϊ���㣿
���𰸡���1��6��78����2������������3��240��
��������
��1�����������Ƶ���ֲ����е����ݿ������a��ֵ���������ݵ���λ����
��2�����ݣ�1����a��ֵ�ͷֲ����гɼ�Ϊ76��x��84��Ƶ�����Խ�Ƶ���ֲ�ֱ��ͼ����������
��3������Ƶ���ֲ����е����ݿ��Լ�������������ѧ�����ж�����ѧ���ı����ɼ�Ϊ���㣮
�⣺��1��a��40��4��8��12��10��6��
�ߵ�3��12��ѧ���ı����ɼ�Ϊ��76��76��78��78��78��78��78��78��80��80��80��82��
�������78��
�ʴ�Ϊ��6��78��
��2���ɣ�1��֪a��6��
��ȫ��Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ��
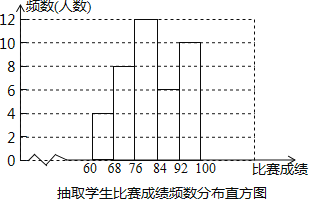
��3��600��![]() ��240��������
��240��������
�𣺽��������ѧ������240��ѧ���ı����ɼ�Ϊ���㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2011ɽ�����ϣ�27��9�֣���ͼ������OABC�У���OΪԭ�㣬��A������Ϊ��0��8������C������Ϊ��6��0����������![]() ����A��C���㣬��AB�߽��ڵ�D��
����A��C���㣬��AB�߽��ڵ�D��
��1���������ߵĺ�������ʽ��
��2����PΪ�߶�BC��һ�����㣨�����C�غϣ�����QΪ�߶�AC��һ�����㣬AQ=CP������PQ����CP=m����CPQ�����ΪS��
����S����m�ĺ�������ʽ�������mΪ��ֵʱ��Sȡ�����ֵ��
����S���ʱ����������![]() �ĶԳ���l�������ڵ�F��ʹ��FDQΪֱ�������Σ���ֱ��д�����з���������F�����ꣻ�������ڣ���˵�����ɣ�
�ĶԳ���l�������ڵ�F��ʹ��FDQΪֱ�������Σ���ֱ��д�����з���������F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˻�ǰij���Ҫ��������ɣ��Ӷ������ð�����ɣ��ҶӶ�����Ҫ����4�죬�����Ӻ���3������µĹ��������ҶӶ�������������ǰһ����ɣ�
��1�����ʸù��������Ƕ����죿
��2����֪��ÿ���ʩ������Ϊ1000Ԫ���Ҷ�ÿ���ʩ������Ϊ800Ԫ��Ҫʹ����̵��ܷ��ò�����7000Ԫ���Ҷ����ʩ�������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() .
.
(1)֤��:����![]() ȡ��ֵ���ú���ͼ����
ȡ��ֵ���ú���ͼ����![]() �����й�����;
���������;
(2)���ú�����ͼ����![]() �ύ�ڵ�(0,3)������������겢�����ú���ͼ��;
�ύ�ڵ�(0,3)������������겢�����ú���ͼ��;
(3)��(2)�������£��۲�ͼ�����������:
�ٲ���ʽ![]() �ĵĽ⼯�� ;
�ĵĽ⼯�� ;
����һԪ���η���![]() ����������ȵ�ʵ��������
����������ȵ�ʵ��������![]() ��ȡֵ��Χ�� ;
��ȡֵ��Χ�� ;
����һԪ���η���![]() ��
��![]() �ķ�Χ����ʵ��������
�ķ�Χ����ʵ��������![]() ��ȡ
��ȡ
ֵ��Χ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
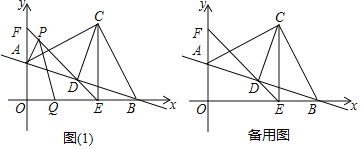
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�A����ABΪб��������ֱ�ǡ�ABC��ʹ��C���ڵ�һ���ޣ�����C��CD��AB�ڵ�D����CE��x���ڵ�E������ED���ӳ���y���ڵ�F��
x+2��x�ύ�ڵ�B����y�ύ�ڵ�A����ABΪб��������ֱ�ǡ�ABC��ʹ��C���ڵ�һ���ޣ�����C��CD��AB�ڵ�D����CE��x���ڵ�E������ED���ӳ���y���ڵ�F��
��1����ͼ��1������PΪ�߶�EF��һ�㣬��QΪx����һ�㣬��AP+PQ����Сֵ��
��2����ֱ��l����ƽ�ƣ���ƽ�ƺ��ֱ��Ϊl1����ֱ��l1��ֱ��AC�ཻ�ڵ�M����y���ཻ�ڵ�N���Ƿ���������ĵ�M����N��ʹ�á�CMNΪ����ֱ�������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OPƽ����BOA��PC��OA��PD��OB������ֱ���C��D�������н����д�����ǣ�������

A. PC=PD B. OC=OD C. OC=OP D. ��CPO=��DPO
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�G����F��CD��һ�㣬������![]() ������AF���ӳ�����O�ڵ�E������AD��DE����CF=2��AF=3���������н��ۣ�
������AF���ӳ�����O�ڵ�E������AD��DE����CF=2��AF=3���������н��ۣ�
�١�ADF�ס�AED����FG=2����tan��E=![]() ����S��DEF=4
����S��DEF=4![]() ��
��
������ȷ���ǣ�������
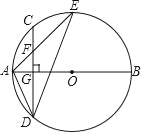
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���е㣬����E��EF��AB����BC�ڵ�F��
��1����֤���ı���DBFE��ƽ���ı��Σ�
��2������ABC����ʲô����ʱ���ı���DBEF�����Σ�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC�ǡ�O��ֱ������BD��AO��E������BC������O��OF��BC��F����BD=8cm��AE=2cm����OF�ij����ǣ�������

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com