
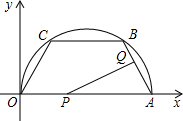
 P点从O点出发,以2cm/s的速度向A运动;同时,Q从A点出发,沿边AB向B以1cm/s的速度运动.
P点从O点出发,以2cm/s的速度向A运动;同时,Q从A点出发,沿边AB向B以1cm/s的速度运动.| AP |
| AO |
| AQ |
| AB |
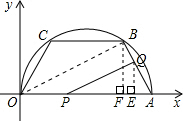 解:(1)如图,连接OB,
解:(1)如图,连接OB,
| ||
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| ||
| 2 |
| AP |
| AO |
| AQ |
| AB |
| 6-2x |
| 6 |
| x |
| 3 |
 |
| OC |
 |
| AB |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
27
| ||
| 4 |
| ||
| 2 |
| 3 |
| 2 |
45
| ||
| 8 |
| 3 |
| 2 |
45
| ||
| 8 |


科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:059
学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图)

(1)按照这种规定填写下表:
(2)根据表中的数据,将s作为纵坐标,n作为横坐标,在如图所示的平面直角坐标系中找出相应各点.

(3)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数图象上,求出该函数的解析式,并利用你探求的结果,求出当n=10时,s的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山西省九年级上学期期末考试数学试卷(解析版) 题型:解答题
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C( ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
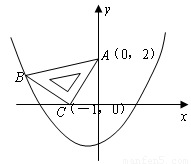
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:专项题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com