
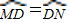 ,EH-HF=2.设∠ACB=a,tana=
,EH-HF=2.设∠ACB=a,tana= ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
 ,结合EH=8,可求AH,再利用勾股定理可求AE,在Rt△AHF中,利用勾股定理可求AF,在Rt△ABD中,由于tan∠1=
,结合EH=8,可求AH,再利用勾股定理可求AE,在Rt△AHF中,利用勾股定理可求AF,在Rt△ABD中,由于tan∠1= ,可设AB=3m,BD=4m,利用勾股定理可知AD=5m,而H是OD中点,从而AD=
,可设AB=3m,BD=4m,利用勾股定理可知AD=5m,而H是OD中点,从而AD= AH,由于AH=6,可求AD、m的值,从而可求AB,利用∠α=∠E,再加上一个公共角,可证△ABC∽△AFE,可得比例线段,容易求出BC.
AH,由于AH=6,可求AD、m的值,从而可求AB,利用∠α=∠E,再加上一个公共角,可证△ABC∽△AFE,可得比例线段,容易求出BC. 解:(1)依题意,及一元二次方程根与系数关系,得
解:(1)依题意,及一元二次方程根与系数关系,得 ,
,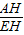 =tana=
=tana= ,又EH=8,
,又EH=8,
 =tana=
=tana= ,
, AD
AD AH=
AH= ×6=8
×6=8 ,
, ,
,
 ;
; ,
, .
.

 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 )和(0,-
)和(0,- ).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.
).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.查看答案和解析>>
科目:初中数学 来源:2002年北京市朝阳区中考数学试卷(解析版) 题型:解答题
 )和(0,-
)和(0,- ).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.
).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《锐角三角函数》(04)(解析版) 题型:解答题
 时,sinB=
时,sinB=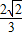 ;
;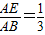 时,sinB=
时,sinB=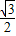 (提示:
(提示: =
=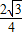 );
);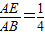 时,sinB=
时,sinB= .
. 时,sinB的值等于______
时,sinB的值等于______查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《锐角三角函数》(02)(解析版) 题型:选择题

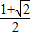

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《图形的相似》(06)(解析版) 题型:解答题
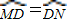 ,EH-HF=2.设∠ACB=a,tana=
,EH-HF=2.设∠ACB=a,tana= ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.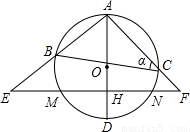
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com