
【题目】如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为_____.

【答案】3或3![]()
【解析】分析:
连接AC、BD相交于点P,由已知条件易得AC=![]() ,BD=6,再根据题意,分①点F由点B向点C运动;②点F由点C向点B运动两种情况,结合已知条件进行分析解答即可.
,BD=6,再根据题意,分①点F由点B向点C运动;②点F由点C向点B运动两种情况,结合已知条件进行分析解答即可.
详解:
如图,连接AC、BD相交于点P,
∵四边形ABCD是菱形,AB=6,∠DAB=60°,
∴∠BAC=30°,AC=2AP,BD=2PB,△ABD和△CBD都是等边三角形,
∴AP=AB·cos30°=![]() ,BP=AB·sin30°=3,AD=BD=CD,
,BP=AB·sin30°=3,AD=BD=CD,
∴AC=![]() .
.
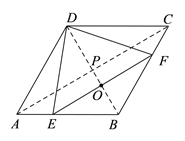
(1)若点F是由点B向点C运动的,则由图1和题意可知,当点E与点A重合时,点F与点B重合,此时点O与线段AB的中点M重合;而当点E移动到与点B重合时,点F移动到与点C重合,此时点O与线段BC的中点N重合,
∴在点E由点A向点B移动,且点F由点B向点C移动的过程后,线段EF的中点O移动所经过的路线是△ABC的中位线MN,
∴在这种情况下,点O移动的路程=MN=![]() AC=
AC=![]() ;
;
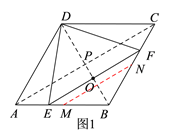
(2)若点F是由点C向点B运动的,则由图2和题意可知,当点E与点A重合时,点F与点C重合,此时点O与点P重合;而当点E移动到与点B重合时,点F也移动到与点B重合,此时点O与点B重合,
∴在点E由点A向点B移动,且点F由点C向点B移动的过程中,线段EF的中点O移动所经过的路线是线段PB,
∴在这种情况下,点O移动的路程=PB=3.

故答案为:![]() 或3.
或3.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
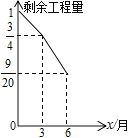
【题目】在青山区“海绵城市”工程中,某工程队接受一段道路施工的任务,计划从2016年10月初至2017年9月底(12个月)完成.施工3个月后,实行倒计时,提高工作效率,剩余工程量与施工时间的关系如图所示,那么按提高工作效率后的速度做完全部工程,则工期可缩短________个月.
查看答案和解析>>
科目:初中数学 来源: 题型:
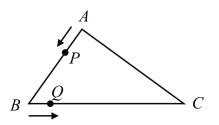
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿![]() 的方向运动,点
的方向运动,点![]() 从点
从点![]() 沿
沿![]() 的方向与点
的方向与点![]() 同时出发;当点
同时出发;当点![]() 第一次回到
第一次回到![]() 点时,点
点时,点![]() ,
,![]() 同时停止运动;用
同时停止运动;用![]() (秒)表示运动时间.
(秒)表示运动时间.
(1)当![]() 为多少时,
为多少时,![]() 是
是![]() 的中点;
的中点;
(2)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,是否存在
个单位长度/秒,是否存在![]() 的值,使得
的值,使得![]() ;
;
(3)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,当点
个单位长度/秒,当点![]() ,
,![]() 是
是![]() 边上的三等分点时,求
边上的三等分点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
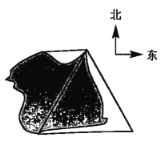
【题目】如图所示,某湖上风景区有两个观望点A,C和两个度假村B、D;度假村D在C正西方向,度假村B在C的南偏东![]() 方向,度假村B到两个观望点的距离都等于2km.
方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A、B、C、D的位置,并写出道路CD与CB的夹角.
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长.
(3)根据题目中的条件,能够判定![]() 吗?若能,请写出判断过程;若不能,请你添加一个条件,判定
吗?若能,请写出判断过程;若不能,请你添加一个条件,判定![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
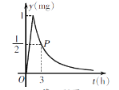
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
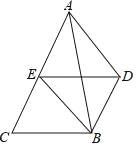
【题目】如图,已知DB∥AC,E是AC的中点,DB=AE,连结AD、BE.
(1)求证:四边形DBCE是平行四边形;
(2)若要使四边形ADBE是矩形,则△ABC应满足什么条件?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市移动通讯公司开设了两种通讯业务,A类是固定用户:先缴50元月租费,然后每通话1分钟再付话费0.4元;B类是“神州行”用户:使用者不缴月租费,每通话1分钟付话费0.6元(这里均指市内通话)。如果一个月内通话时间为x分钟,分别设A类和B类两种通讯方式的费用为y![]() 元和y
元和y![]() 元,
元,
(1)写出y![]() 、y
、y![]() 与x之间的函数关系式。
与x之间的函数关系式。
(2)一个月内通话多少分钟,用户选择A类合算?B类呢?
(3)若某人预计使用话费150元,他应选择哪种方式合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,AC是⊙O的直径,D为⊙O上一点,过D作⊙O的切线交BA的延长线于P,且DP⊥BP于P.若PD+PA=6,AB=6,则⊙O的直径AC的长为( )
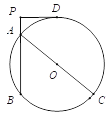
A. 5 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com