
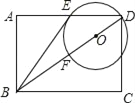
【题目】已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.
(1)判断直线BE与⊙O的位置关系,并证明你的结论;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
【答案】(1)直线BE与⊙O相切,证明见解析;(2)⊙O的半径为![]() .
.
【解析】分析:(1)连接OE,根据矩形的性质,可证∠BEO=90°,即可得出直线BE与⊙O相切;
(2)连接EF,先根据已知条件得出BD的值,再在△BEO中,利用勾股定理推知BE的长,设出⊙O的半径为r,利用切线的性质,用勾股定理列出等式解之即可得出r的值.
详解:(1)直线BE与⊙O相切.理由如下:
连接OE,在矩形ABCD中,AD∥BC,∴∠ADB=∠DBC.
∵OD=OE,∴∠OED=∠ODE.
又∵∠ABE=∠DBC,∴∠ABE=∠OED,
∵矩形ABDC,∠A=90°,∴∠ABE+∠AEB=90°,
∴∠OED+∠AEB=90°,∴∠BEO=90°,∴直线BE与⊙O相切;
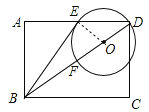
(2)连接EF,方法1:
∵四边形ABCD是矩形,CD=2,∴∠A=∠C=90°,AB=CD=2.
∵∠ABE=∠DBC,∴sin∠CBD=![]()
∴![]() ,
,
在Rt△AEB中,∵CD=2,∴![]() .
.
∵tan∠CBD=tan∠ABE,∴![]() ,
,
由勾股定理求得![]() .
.
在Rt△BEO中,∠BEO=90°,EO2+EB2=OB2.
设⊙O的半径为r,则![]() ,∴r=
,∴r=![]() ,
,
方法2:∵DF是⊙O的直径,∴∠DEF=90°.
∵四边形ABCD是矩形,∴∠A=∠C=90°,AB=CD=2.
∵∠ABE=∠DBC,∴sin∠CBD=![]() .
.
设![]() ,则
,则![]() .
.
span>∵CD=2,∴![]() .
.
∵tan∠CBD=tan∠ABE,∴![]() ,
,
∴E为AD中点.
∵DF为直径,∠FED=90°,∴EF∥AB,∴![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处(
处(![]() ),一边
),一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.

(1)将图1中的三角板绕点![]() 逆时针旋转至图2,使一边
逆时针旋转至图2,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,求
,求![]() 的度数;
的度数;
(2)将图1中的三角板绕点![]() 以每秒5的速度沿逆时针方向旋转一周,在旋转的过程中,第
以每秒5的速度沿逆时针方向旋转一周,在旋转的过程中,第![]() 秒时,直线
秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() ,求
,求![]() 的值;
的值;
将图1中的三角板绕点![]() 逆时针旋转至图3,使一边
逆时针旋转至图3,使一边![]() 在
在![]() 的内部,请探究
的内部,请探究![]() 的值./span>
的值./span>
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
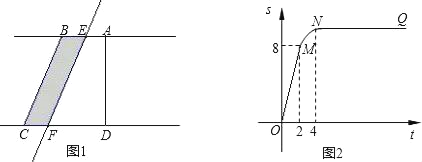
信息读取
(1)梯形上底的长AB= ;
(2)直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地发生地震,学校师生积极捐款,已知第一天捐款4800元,第二天捐款6000元,第二天捐款人数比第一天捐款人数多50人,且两天人均捐款数相等。
(1)求第二天参加捐款的人数是多少?
(2)第三天又有100人捐款,第三天人均捐款数与前两天相同,求第三天捐款数额
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(阅读材料)
在数轴上,通常用“两数的差”来表示“数轴上两点的距离”如图1中三条线段的
长度可表示为:![]() ,
,![]() 结论:数轴上任意两点
结论:数轴上任意两点
表示的数为分别![]() ,则这两个点间的距离为
,则这两个点间的距离为![]() (即:用较大的数去减较小的数)
(即:用较大的数去减较小的数)
![]()
(理解运用)
根据阅读材料完成下列各题:
(1)如图2, ![]() 分别表示数
分别表示数![]() ,求线段
,求线段![]() 的长;
的长;
![]()
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 对应的数值.
对应的数值.
(3)![]() 两点分别从
两点分别从![]() 同时出发以3个单位、2个单位长度的速度沿数轴向右运动,求当点
同时出发以3个单位、2个单位长度的速度沿数轴向右运动,求当点![]() 重合时,它们运动的时间;
重合时,它们运动的时间;
(4)在(3)的条件下,求当![]() 时,它们运动的时间.
时,它们运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
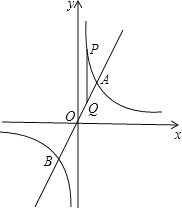
【题目】如图,已知直线y=kx(k>0)与双曲线![]() 交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点
交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点![]() ,过点P作PQ//y轴交直线AB于点Q.
,过点P作PQ//y轴交直线AB于点Q.
(1)直接写出k的值及点B的坐标:
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从![]() 、
、![]() 出发,沿直线轨道同时到达
出发,沿直线轨道同时到达![]() 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与
处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与![]() 处的距离
处的距离![]() 、
、![]() (米)与时间
(米)与时间![]() (分钟)的函数关系如图所示,则下列结论中:①
(分钟)的函数关系如图所示,则下列结论中:①![]() 的距离为120米;②乙的速度为60米/分;③
的距离为120米;②乙的速度为60米/分;③![]() 的值为
的值为![]() ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的
;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的![]() 的取值范围是
的取值范围是![]() ,其中正确的有( )个
,其中正确的有( )个
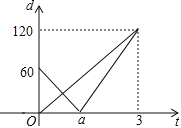
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com