小明和小红在一本数学资料书上看到有这样一道竞赛题:“已知△ABC的三边长分别为a,b,c,且|b+c-2a|+(b+c-5)2=0,求b的取值范围”.
(1)小明说:“b的取值范围,我看不出如何求,但我能求出a的长度.”你知道小明是如何计算的吗?你帮他写出求解的过程.
(2)小红说:“我也看不出如何求b的范围,但我能用含b的代数式表示c”.同学,你能吗?若能,帮小红写出过程.
(3)小明和小红一起去问数学老师,老师说:“根据你们二人的求解,利用书上三角形的三边满足的关系,即可求出答案.”你知道答案吗?请写出过程.
解:(1)∵|b+c-2a|+(b+c-5)
2=0,
∴b+c-2a=0且b+c-5=0,
∴2a=5,解得a=

;
(2)由b+c-5=0,得c=5-b;
(3)由三角形的三边关系,得
当5-b≥

,即b≤

时,则
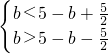
,解得

<b≤

;
当5-b<

时,即b>

,则
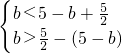
,解得

<b<

,
∴b的取值范围为

<b<

.
分析:(1)根据平方和绝对值的非负性,可得b+c-2a=0且b+c-5=0,把b+c看作一个整体,两个方程相减即可得a的值.
(2)由b+c-5=0,直接移项,可得用含b的代数式表示c的式子.
(3)由(1)(2)可知,a=

,c=5-b,根据三角形的三边关系,两边之和大于第三边且两边之差小于第三边,列不等式组,求出b的取值范围.
点评:已知三角形的两边,则第三边a的取值范围是“两边之差<a<两边之和”.

 ;
; ,即b≤
,即b≤ 时,则
时,则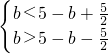 ,解得
,解得 <b≤
<b≤ ;
; 时,即b>
时,即b> ,则
,则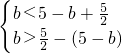 ,解得
,解得 <b<
<b< ,
, <b<
<b< .
. ,c=5-b,根据三角形的三边关系,两边之和大于第三边且两边之差小于第三边,列不等式组,求出b的取值范围.
,c=5-b,根据三角形的三边关系,两边之和大于第三边且两边之差小于第三边,列不等式组,求出b的取值范围.

 名校课堂系列答案
名校课堂系列答案