
(本题12分) 在正方形网格中以点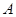 为圆心,
为圆心, 为半径作圆
为半径作圆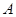 交网格于点
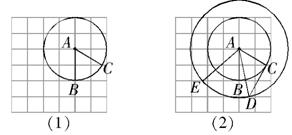
交网格于点 (如图(1)),过点
(如图(1)),过点 作圆的切线交网格于点
作圆的切线交网格于点 ,以点
,以点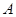 为圆心,
为圆心, 为半径作圆交网格于点
为半径作圆交网格于点
(如图(2)).
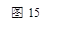 问题:
问题:
(1)求 的度数;
的度数;
(2)求证: 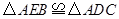 ;
;
(3) 可以看作是由
可以看作是由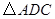 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断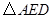 的形状(不用说明理由).
的形状(不用说明理由).
(4)如图(3),已知直线 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形 ,使三个顶点
,使三个顶点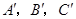 ,分别在直线
,分别在直线 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.

(1)连接BC,由网格可知点C在AB的中垂线上,
∴AC=BC,…………………………………………………………………………………1分
∵AB=AC,
∴AB=BC=AC,即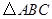 是等边三角形.……………………………………………2分
是等边三角形.……………………………………………2分
∴ =60°;…………………………………………………………………………3分
=60°;…………………………………………………………………………3分
(2)∵CD切⊙A于点C,
∴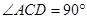
 .…………………………………………………………………4分
.…………………………………………………………………4分
在Rt 与Rt
与Rt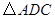 中,
中,
∵AB=AC,AE=AD.……………………………………………………………………5分
∴ 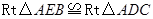 (HL).……………………………………………………6分
(HL).……………………………………………………6分
(3) 可以看作是由
可以看作是由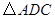 绕点A顺时针旋转60°得到的. …………7分
绕点A顺时针旋转60°得到的. …………7分 是等边三角形.………………………………………………………………8分
是等边三角形.………………………………………………………………8分
(4)在直线a上任取一点,记为点A′,作A′M′⊥b,垂足为点M′;作线段
A′M′的垂直平分线,此直线记为直线d;以点A′为圆心,A′M′长为半径画圆,与直线d交于点N′;………………………9分
过点N′作N′C′⊥A′N′交直线c于点C′;……………………………………10分
以点A′为圆心,A ′C′ 长为半径画圆,此圆交直线b于点B′; ……………11分
连接A′B′、B′C′,则△A′B′C′为所求等边三角形.………………………12分
【解析】略


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
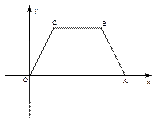
(本题12分)如图,在平面直角坐标系中,等腰梯形OABC,CB//OA,且点A在x轴正半轴上.已知C(2,4),BC=4.
(1)求过O、C、B三点的抛物线解析式,并写出顶点坐标和对称轴;
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合),使得P点到两坐标轴的
距离相等.如果存在,求出P点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 轴、
轴、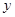 轴的正半轴上,点A在双曲线
轴的正半轴上,点A在双曲线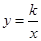 的
的
 值;
值;查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届浙江临安於潜第一初级中学九年级上期末综合考试数学试卷(一)(带解析) 题型:解答题
(本题12分)
某商品的进价为每千克40元,销售单价与月销售量的关系如下表(每千克售价不能高于65元):
| 销售单价(元) | 50 | 53 | 56 | 59 | 62 | 65 |
| 月销售量(千克) | 420 | 360 | 300 | 240 | 180 | 120 |
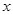 元(
元(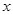 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为 元.
元. 与
与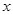 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量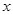 的取值范围;
的取值范围;查看答案和解析>>
科目:初中数学 来源:2012届九年级第三次模拟考试数学卷 题型:解答题
(本题满分12分)在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t. 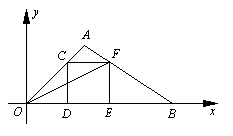
【小题1】⑴ 求tan∠FOB的 值;
值;
【小题2】⑵用含t的代数式表示△OAB的面积S;
【小题3】⑶是否存在点C,使以B,E,F为顶点的三角形与△OFE相似,若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com