
����Ŀ����������ͼ���������� ABCD �У�P �� CD ��һ���㣨�� C��D ���غ�����ʹ���ǰ��ֱ�Ƕ������ P �غϣ�����һ��ֱ�DZ�ʼ�վ����� B����һֱ�DZ��������ε�ijһ������ֱ�߽��ڵ� E��
��1�����ݲ����������������������ͼ�Σ�
��2���۲�����ͼ�Σ�д��һ�����BPC ���Ƶ������Σ���˵�����ɣ�
��3������ P λ�� CD ���е�ʱ��ֱ��д����2�����������������ε����Ʊȣ�
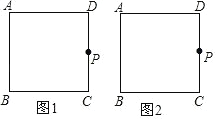
���𰸡���1����ͼ��ʾ����������2�����ۣ���PBC�ס�EPD�����ɼ���������3�����Ʊȣ�2��1��
��������
��1������Ҫ��ͼ�μ��ɣ� (2)���ۣ���PBC�ס�EPD���������Ƕ�Ӧ��ȵ��������������Ƽ���֤���� (3) �������������ε����ʼ��ɽ������.
��1����ͼ��ʾ��

��2�����ۣ���PBC�ס�EPD��
���ɣ����ı��� ABCD �������Σ�
���D����C��90�㣬
�ߡ�BPE��90�㣬
���BPC+��EPD��90�㣬��EPD+��PED��90�㣬
���BPC����PED��
���PBC�ס�EPD��
�ߡ�PBC�ס�EPD��
�����Ʊȣ�BC��PD��
��BC��CD��PD��PC��
�����Ʊȣ�2��1��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
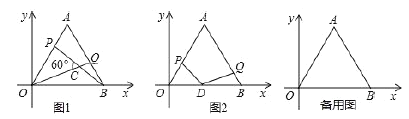
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊԭ�㣬
Ϊԭ�㣬![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
�� ![]() ���ϵĶ��㣬��
���ϵĶ��㣬��![]() ����
����![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ��������
��������![]() ��
��![]() ����λÿ����ٶȴӵ�
����λÿ����ٶȴӵ�![]() ���
���![]() �˶�����
�˶�����![]() ��2����λÿ����ٶȴӵ�
��2����λÿ����ٶȴӵ�![]() ���
���![]() �˶������˶�ʱ��Ϊ
�˶������˶�ʱ��Ϊ![]() ��
��
(1)��ͼ1����֪���![]() ����Ϊ
����Ϊ![]() ��������
��������![]() ����
����![]() ������:
������:
(2)��ͼ1������![]() ��
��![]() ���ڵ�
���ڵ�![]() �����ʵ�
�����ʵ�![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
(3)��ͼ2��![]() Ϊ
Ϊ![]() ���ϵ��е㣬
���ϵ��е㣬![]() ��
��![]() ���˶������У�
���˶������У�![]() ��
��![]() ��
��![]() �����Ƿ��ܹ���ʹ
�����Ƿ��ܹ���ʹ![]() �ĵ��������Σ����ܣ�����:���˶�ʱ��
�ĵ��������Σ����ܣ�����:���˶�ʱ��![]() ���ڴ�ʱ�ı���
���ڴ�ʱ�ı���![]() �����:�����ܣ���˵�����ɣ�
�����:�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���߲�ÿǧ���ۼ�![]() ��Ԫ���������·�
��Ԫ���������·�![]() ֮��Ĺ�ϵ��ͼ1��ʾ��ÿǧ�˳ɱ�
֮��Ĺ�ϵ��ͼ1��ʾ��ÿǧ�˳ɱ�![]() ��Ԫ���������·�
��Ԫ���������·�![]() ֮��Ĺ�ϵ��ͼ2��ʾ������ͼ1�еĵ���ͬһ���߶��ϣ�ͼ2�еĵ���ͬһ���������ϣ��������ߵ���͵������Ϊ��6��1����
֮��Ĺ�ϵ��ͼ2��ʾ������ͼ1�еĵ���ͬһ���߶��ϣ�ͼ2�еĵ���ͬһ���������ϣ��������ߵ���͵������Ϊ��6��1����
��1�����![]() ��
��![]() ֮������ĺ�������ʽ����ֱ��д��
֮������ĺ�������ʽ����ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����![]() ��
��![]() ֮������ĺ�������ʽ��
֮������ĺ�������ʽ��
��3���������߲�ÿǧ������Ϊ![]() Ԫ���������ĸ��·ݳ��������߲ˣ�
Ԫ���������ĸ��·ݳ��������߲ˣ�![]() ��ȡ�����ֵ������������ֵ��������=�ۼ�-�ɱ���
��ȡ�����ֵ������������ֵ��������=�ۼ�-�ɱ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
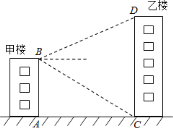
����Ŀ����֪��¥��![]() �ף��Լ�¥¥��
�ף��Լ�¥¥��![]() ������¥¥��
������¥¥��![]() ������Ϊ
������Ϊ![]() ������¥¥��
������¥¥��![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ����Ҫ����¥¥��
����Ҫ����¥¥��![]() ��
��![]() ֮����һ���������¥�ĸ߶�
֮����һ���������¥�ĸ߶�![]() �Լ����
�Լ����![]() �ij��ȣ����������ȷ��
�ij��ȣ����������ȷ��![]() �ף�
�ף�
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�����OABC�Ķ���O������ԭ���غϣ�A��C�ֱ����������ϣ���B������Ϊ��4��2����ֱ��![]() ��AB��BC�ֱ��ڵ�M��N������������
��AB��BC�ֱ��ڵ�M��N������������![]() ��ͼ����M��N��
��ͼ����M��N��

��1�����������Ľ���ʽ��
��2������P��y���ϣ�����OPM��������ı���BMON�������ȣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D�ǵȱ���ABC�ı�BC���е㣬E��F�ֱ���AB��AC�ϣ���EDF+��A=180����AE:EB=5:1��EF=![]() ����CF��Ϊ__________��
����CF��Ϊ__________��
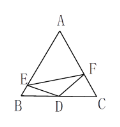
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������300ǧ�ף��ס�������ͬʱ��A�س������Ը��Ե��ٶ�������B����ʻ���׳��ȵ���B�أ�ͣ��1Сʱ���ٶȲ��䣬��ԭ·���أ���������ʻ��ʱ����xСʱ���뿪A�صľ�����yǧ�ף���ͼ��y��x�ĺ���ͼ��
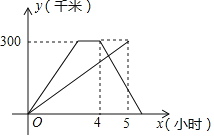
��1���׳����ٶ����������ҳ����ٶ���������
��2���׳��ڷ���;�У��������20ǧ��ʱ�����ҳ���ʻ��ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ĸ��߷ֱ�ƽ����
�ĸ��߷ֱ�ƽ����![]() ���
���![]() �ᣬ���ҷֱ���
�ᣬ���ҷֱ���![]() ��ͬʱ�������ؾ���
��ͬʱ�������ؾ���![]() �ı��������˶��װ���ʱ�뷽����
�ı��������˶��װ���ʱ�뷽����![]() ����λ/����ٶ������˶����Ұ�˳ʱ�뷽����
����λ/����ٶ������˶����Ұ�˳ʱ�뷽����![]() ����λ/����ٶ������˶�����ס����˶���ĵ�
����λ/����ٶ������˶�����ס����˶���ĵ�![]() �������ص�������ǣ� ��
�������ص�������ǣ� ��

A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
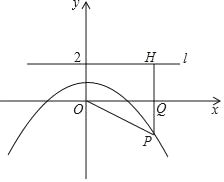
����Ŀ����ͼ��P��m��n����������y=��![]() +1������һ�㣬l�ǹ��㣨0��2������x��ƽ�е�ֱ�ߣ�����P��ֱ��PH��l������ΪH��PH��x����Q��
+1������һ�㣬l�ǹ��㣨0��2������x��ƽ�е�ֱ�ߣ�����P��ֱ��PH��l������ΪH��PH��x����Q��
��1����̽������գ���m=0ʱ��OP=�� ����PH=�� ������m=4ʱ��OP=�� ����PH=�� ����
��2����֤����������m��n������OP��PH�Ĵ�С��ϵ����֤����IJ��룮
��3����Ӧ�ã���OP=OH����m��0ʱ����P������꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com