
【题目】如图,已知∠ABC,①BD平分∠ABC;②DE=DF;③∠ABC+∠EDF=180°,以①②③中的两个作为条件,另一个作为结论,可以使结论成立的有几个( )

A.0个B.1个C.2个D.3个
【答案】D
【解析】
过D作DM⊥AB于M,DN⊥BC于N,分三种情况,分别推出△END≌△FMD即可.
如图:作DM⊥BA于点M,DN⊥BC于点N,

(1)①BD平分∠ABC;②DE=DF;作为条件,③∠ABC+∠EDF=180°作为结论
因为BD平分∠ABC, DM⊥BA,DN⊥BC,
所以DM=DN,∠DNE=∠DMF= 90°
又因为DE=DF,
所以△DEN≌△DFM
所以∠DEN=∠DFM,
因为∠DEB +∠CED =180°,
所以∠DEB +∠BFD= 180°
所以在四边形BEDF中,
∠ABC+∠EDF = 360°-180°= 180°,
即∠ABC+∠EDF = 180° (3) 作为结论成立;
(2) ①BD平分∠ABC;③∠ABC+∠EDF=180°;作为条件,②DE=DF作为结论
因为BD平分∠ABC, DM⊥BA,DN⊥BC,
所以DM=DN,∠DNE=∠DMF= 90°,
因为∠ABC+∠EDF=180°,
所以在四边形BEDF中,∠DEB +∠BFD = 360°- 180°= 180°,
因为∠DEB +∠CED =180°,
所以∠DEN=∠DFM
所以△DEN≌△DFM
所以DE=DF, (2) 作为结论成立;
(3) ②DE=DF;③∠ABC+∠EDF=180°;作为条件,①BD平分∠ABC作为结论
因为∠ABC+∠EDF=180°,
所以在四边形BEDF中,∠DEB +∠BFD = 360°- 180°= 180°,
因为∠DEB +∠CED =180°,
所以∠DEN=∠DFM
因为DM⊥BA,DN⊥BC,
所以∠DNE=∠DM F= 90°,
因为DE=DF
所以△DEN≌△DFM
所以DM=DN
因为DM⊥BA,DN⊥BC, DM=DN
所以BD平分∠ABC(1) 作为结论成立;
故:有3种情况满足题干要求
故选:D


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
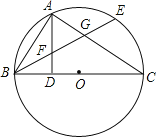
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC和△DEF,下列条件中①∠B=∠E=90°,AC=DF;②∠B=∠E,AB=DE,AC=DF;③在Rt△ABC和Rt△DEF中,BC=EF,AC=DF;④∠A=∠D,∠B=∠E,∠C=∠F;⑤∠A=∠D,BC=EF,∠C=∠F,能证明△ABC≌△DEF的是( )

A.③⑤B.①③⑤C.①②③⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠C=90°,∠A=30°,AB边中点D到BC边距离为3 cm,现在AC边找点E,使BE+ED值最小,则BE+ED的最小值是________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△AOB的顶点O在直线上,且AO=AB.
(1)画出△AOB关于直线成轴对称的图形△COD,且使点A的对称点为点C;
(2)在(1)画出的图形中,AC与BD的位置关系是 ;
(3)在(1)画出的图形中连接AD,如果∠ABD=2∠ADB.
求证:△AOC是等边三角形,并直接写出∠DAO∶∠DAB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com