
(2005 哈尔滨)如图所示,点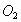 是
是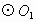 上一点,
上一点,![]() 与
与 相交于A、D两点,BC⊥AD,垂足为D,分别交
相交于A、D两点,BC⊥AD,垂足为D,分别交 、
、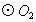 于B、C两点,延长
于B、C两点,延长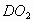 交
交![]() 于E,交BA的延长线于F,
于E,交BA的延长线于F,![]() 交AD于G,连接AC.
交AD于G,连接AC.

(1)求证:∠BGD=∠C;
(2)若![]() =45°,求证:AD=AF
=45°,求证:AD=AF
(3)若BF=6CD,且线段BD、BF的长是关于x的方程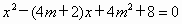 的两个实数根,求BD、BF的长.
的两个实数根,求BD、BF的长.
|
解 (1)∵BC⊥AD于D,∴∠ BDA=∠CDA=90°,∴ AB、AC分别为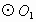 、 、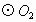 的直径. 的直径.
如图,∵∠ 2=∠3,∠BGD+∠2=90°,∠C+∠3=90°,∴∠BGD=∠C.
(2) ∵
∴∠4=22.5°, ∵ ∴AD=AF (3)如图
设CD=k,∵BF=6CD,∴BF=6k 连接AE,则
∴AE·BF=BD·AF 又∵在△AO2E和△DO2C中,AO2=DO2,∠AO2E=∠DO2C,O2E=O2C, △AO2E≌△DO2C,∴AE=CD=k,∴6k2=BD·AF=(BC-CD)(BF-AB) ∵∠BO2A=90°,AO2=CO2 ∴BC=AB,∴6k2=(BC-k)(6k-BC) ∴BC2-7kBC+12k2=0 解得,BC=3k,或BC=4k 当BC=3k时,BD=2k ∵BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根 ∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2,BD·BF=12k2 =4m2+8, 整理得:4m2-12m+29=0 ∵△=(-12)2-4×4×29=-320<0,此方程无实数根,BC=3k不成立。 当BC=4k时,BD=3k, ∴3k+6k=4m+2, ∴原方程可化为 解得:
|
|
点评 这是一个以几何为背景的综合题,综合二次函数以及三角形、圆等知识,知识面广,综合性强,从中可以看出考生能力的高低. |


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:013
(2005·哈尔滨)已知两个一次函数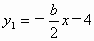 和
和 的图像重合,则一次函数y=ax+b的图像所经过的象限为
的图像重合,则一次函数y=ax+b的图像所经过的象限为
[ ]
查看答案和解析>>
科目:初中数学 来源: 题型:013
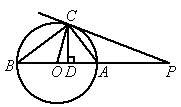
(2005 哈尔滨)如图所示,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①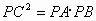 ;②PC·OC=OP·CD;③
;②PC·OC=OP·CD;③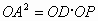 ;④OA(CP-CD)=AP·CD.正确的结论有
;④OA(CP-CD)=AP·CD.正确的结论有
[ ]
|
A.1个 |
B.2个 |
C.3个 |
D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com