练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
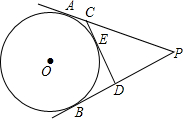
    20．如图，PA、PB切⊙O于点A、B，CD是⊙O的切线，交PA、PB于C、D两点，△PCD的周长是36，则AP的长为（　　）
    A．12B．18C．24D．9

    分析 由于DA、DC、BC都是⊙O的切线，可根据切线长定理，将△PCD的周长转换为PA、PB的长，然后再进行求解即可．

    解答 解：
    ∵PA、PB分别是⊙O的切线，且切点为A、B；
    ∴PA=PB；
    同理，可得：DE=DA，CE=CB；
    则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=36，
    ∴PA=PB=18，
    故选B．

    点评 此题主要考查了切线长定理的应用，能够将△PCD的周长转换为切线PA、PB的长是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

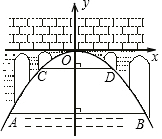    10．有一座抛物线形拱桥，校下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米．
    （1）在如图的坐标系中，求抛物线的表达式；
    （2）若洪水到来是水位以0.2米/时的速度上升，从正常水位开始，再过几小时能到达桥面？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．问题与探索
    问题情境：课堂上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动．如图（1），将一张菱形纸片ABCD（∠BAD＞90°）沿对角线AC剪开，得到△ABC和△ACD．
    操作发现：
    （1）将图（1）中的△ACD以点A为旋转中心，按逆时针方向旋转角α，使α=∠BAC，得到如图（2）所示的△AC′D，分别延长BC和DC′交于点E，则四边形ACEC′的形状是菱形．
    （2）创新小组将图（1）中的△ACD以点A为旋转中心，按逆时针方向旋转角α，使α=2∠BAC，得到如图（3）所示的△AC′D，连接DB、C′C，得到四边形BCC′D，发现它是矩形，请证明这个结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知有理数a、b满足（a-2）2+|b+3|=0，那么代数式ba的值是9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．画一条数轴，将下列各数在此数轴上表示出来，并把这些数用“＜”连接起来．
    -（-1），-|-2|，-3$\frac{1}{2}$，（-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在数轴上A点表示数a，B点表示数b，C点表示数c，b是最小的正整数，且a、b满足|a+2|+（c-7）2=0．
    （1）填空：a=-2，b=1，c=7；
    （2）画出数轴，并把A，B，C三点表示在数轴上；
    （3）P是数轴上一动点，P点表示的数是x，当PA+PB+PC=10时，x=0或2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法中正确的是（　　）
    A．近似数0.66有两个有效数字B．近似数5.01×103精确到百分位
    C．近似数2.10精确到十分位D．近似数5.8万精确到万位

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，在长为100m，宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644m2，则道路的宽应为多少米？设道路的宽为x m，则可列方程为（　　）
    A．100×80-100x-80x=7644B．（100-x）（80-x）+x2=7644
    C．（100-x）（80-x）=7644D．100x+80x-x2=7644

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列四个实数中，最大的是（　　）
    A．-2B．0C．-$\sqrt{2}$D．$\sqrt{3}$

    查看答案和解析>>

    同步练习册答案