
����Ŀ��ij�մɹ�˾�й����ƣ�������˾���˹���ʱ�䣺ÿ�칤��![]() Сʱ��ÿ�¹���
Сʱ��ÿ�¹���![]() �죻���������˰��Ƽ������ʣ�ÿ�����������
�죻���������˰��Ƽ������ʣ�ÿ�����������![]() Ԫ�����½����������ù�˾ֻ�����ס��������մɣ�����С����¼������һЩ���ݣ�
Ԫ�����½����������ù�˾ֻ�����ס��������մɣ�����С����¼������һЩ���ݣ�
�����մ� ����λ������ | �����մ� ����λ������ | ��ʱ�� ����λ�����ӣ� | �Ƽ����� ����λ��Ԫ�� |
|
|
|
|
|
|
|
|
��1��������ÿ�������մ������ʱ��Ϊ![]() ���ӣ��ú���
���ӣ��ú���![]() �Ĵ���ʽ��ʾ����ÿ�������մ������ʱ�䣻
�Ĵ���ʽ��ʾ����ÿ�������մ������ʱ�䣻
��2����С������С��ij�£�����![]() �죩���������մ�
�죩���������մ�![]() ���������մ�
���������մ�![]() ����
����
������![]() ��
��![]() �ĺ�����ϵʽ��������д���Ա���
�ĺ�����ϵʽ��������д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڸ����г����飬ÿ������ÿ�����������մɵ����������������մ�������![]() ����������ÿ�������մɵļƼ����ʿ����
����������ÿ�������մɵļƼ����ʿ����![]() Ԫ�������մɼƼ�����Ҳ����ߵĿռ䣮��С���Ĺ���Ч�ʲ��䣬�����մɼƼ���������Ҫ��߶���Ԫ��С�����¹��ʣ��Ƽ�����+��������
Ԫ�������մɼƼ�����Ҳ����ߵĿռ䣮��С���Ĺ���Ч�ʲ��䣬�����մɼƼ���������Ҫ��߶���Ԫ��С�����¹��ʣ��Ƽ�����+��������![]() �¹��ʣ������쵽
�¹��ʣ������쵽![]() Ԫ��
Ԫ��
���𰸡�(1) ��35-m�����ӣ�(2)��y=![]() x+600���ڼ����մɼƼ���������Ҫ���0.3Ԫ��С�����¹��ʲ����쵽1200Ԫ��
x+600���ڼ����մɼƼ���������Ҫ���0.3Ԫ��С�����¹��ʲ����쵽1200Ԫ��
��������
��1�����������֪������ÿ�������մ�����ʱ��Ϊ��35-m�����ӣ�
��2�������ȸ���ͼ�����з��������һ�������մ��������մɵ�ʱ�䣬�ٸ���һ�µĹ���ʱ�伴����ú�������ʽ��
��������ÿ�������մɼƼ�����ΪaԪ������ÿ�������մɼƼ�����ΪbԪ�����ù���2.8��6.6��Ϊ��ȹ�ϵ�з����飬���![]() ���Ӷ��õ�p��
���Ӷ��õ�p��![]() �����ݷ����������ĵ����Կ�֪��p��x������������������x��500����x=500ʱ��pȡ����Сֵ����ʱp=0.3��
�����ݷ����������ĵ����Կ�֪��p��x������������������x��500����x=500ʱ��pȡ����Сֵ����ʱp=0.3��
��1������ÿ�������մ�����ʱ��Ϊ��35-m�����ӣ�
��2�����������֪��3m+2��35-m��=85
��ã�m=15
������ÿ�������մ�����ʱ�䣺35-m=20����
�������֪��15x+20y=8��25��60
����ã�y=![]() x+600
x+600
��y��x�ĺ�����ϵʽ��y=![]() x+600��
x+600��
��������ÿ�������մɼƼ�����ΪaԪ������ÿ�������մɼƼ�����ΪbԪ��
�������֪��![]() ����ã�
����ã�![]() ��
��
������մɼƼ�����Ҫ���pԪ��С�����¹��ʲ����쵽1200Ԫ
�������֪��1200��(1+p)x+(1.8+0.2)( ![]() x+600)+100
x+600)+100
����ã�p��![]()
��p��![]() �Ƿ�������������k=100��0
�Ƿ�������������k=100��0
��p��x���������С
����p��![]() ��p��x�����������
��p��x�����������
�֡�x��![]() y��x��
y��x��![]() (
(![]() x+600)
x+600)
��ã�x��500
�൱x=500ʱ��pȡ�����ֵ����ʱp=0.3��
�𣺼����մɼƼ���������Ҫ���0.3Ԫ��С�����¹��ʲ����쵽1200Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
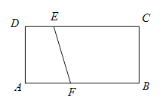
����Ŀ����ͼ���ھ���ABCD�У�AB=4��AD=2����E��CD�ϣ�DE=1����F�DZ�AB��һ���㣬��EFΪб����Rt��EFP������P�ھ���ABCD�ı��ϣ���������ֱ��������ǡ������������AF��ֵ��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ϵ�һ����ѧ��ȤС��![]() ��ѧ���ڱ������µ�������ѧ�ɼ����£�
��ѧ���ڱ������µ�������ѧ�ɼ����£�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���������ݵ���λ����________��ƽ������________��������________��
���������ݵ���λ����________��ƽ������________��������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ͬʱ��ʼ�ӹ�һ����װ���ӿ�ʼ�ӹ������������װ�׳��乤����8Сʱ���ҳ�������;ͣ��һ��ʱ��ά���豸��Ȼ���ڼ׳���ӹ���4Сʱʱ��ͣ��ǰ�Ĺ���Ч�ʼ����ӹ���ֱ����׳���ͬʱ���������װ�ļӹ�������ס�����������Լӹ���װ������Ϊ![]() ���������׳���ӹ���ʱ��Ϊ
���������׳���ӹ���ʱ��Ϊ![]() ��ʱ����
��ʱ����![]() ��
��![]() �ĺ���ͼ����ͼ��ʾ��
�ĺ���ͼ����ͼ��ʾ��
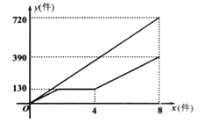
��1���׳���ÿСʱ�ӹ���װ�ļ���Ϊ________����������װ���ܼ���Ϊ________����
��2���ҳ��仨�˶���ʱ��ά���豸��
��3����ס�������������������£���ͬ��ɼӹ�800����װʱ�׳������õ�ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
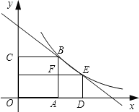
����Ŀ����ͼ��������![]() ��
��![]() �Ķ���
�Ķ���![]() ��
��![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��˫����
��˫����![]() �ϣ�����
�ϣ�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����ֱ��
����ֱ��![]() �ĺ�������ʽΪ________��
�ĺ�������ʽΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��ax![]() +bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x
+bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x![]() ��3x+5����a+b+c=__________��
��3x+5����a+b+c=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬABCD�У�AB=4��BC=8����E��F�ֱ���AD��BC�ϣ���ֽƬABCD��ֱ��EF�۵�����C����AD�ϵ�һ��H������D���ڵ�G�����������ĸ����ۣ���HE=HF����ECƽ����DCH�����߶�BF��ȡֵ��ΧΪ3��BF��4��������H���A�غ�ʱ��EF=2![]() �����Ͻ����У�����Ϊ��ȷ���У�����������
�����Ͻ����У�����Ϊ��ȷ���У�����������
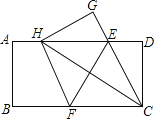
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���̶ӣ��ڹ����б�ʱ���ӵ��ס����������̶ӵ�Ͷ���飬ʩ��һ�죬�踶���̶ӹ��̿�1.2��Ԫ���ҹ��̶ӹ��̿�0.5��Ԫ�� �����쵼С����ݼס������ӵ�Ͷ������㣬�����·�����
��1���ӵ����������̸պ�������ɣ�
��2���Ҷӵ�����������Ҫ�ȹ涨���ڶ���6�죻
��3�����ס������Ӻ���3�죬���µĹ������Ҷӵ�����Ҳ����������ɣ�
���ʣ��ڲ������ڵ�ǰ���£��������һ��ʩ���������ʡ���̿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ�
��4a+b=0����9a+c��3b����8a+7b+2c��0������x����1ʱ��y��ֵ��xֵ�������������������ֵy<0ʱ���Ա���x��ȡֵ��Χ��x<-1��x>5.
������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com