
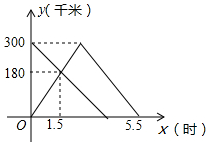
 �ס��������ֱ��A��B����ͬʱ�������׳�����ǰ��B�أ�����B����������һ�ٶȰ�ԭ·���ٷ��ص�A�أ��ҳ�����ǰ��A�أ���ס���������A�ص�·��Ϊy��ǧ�ף����׳���ʻ��ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ��
�ס��������ֱ��A��B����ͬʱ�������׳�����ǰ��B�أ�����B����������һ�ٶȰ�ԭ·���ٷ��ص�A�أ��ҳ�����ǰ��A�أ���ס���������A�ص�·��Ϊy��ǧ�ף����׳���ʻ��ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ������ ��1��������������ʽ���ɵõ����ۣ�
��2�����������з����鼴�ɵõ����ۣ�
��3��������������ʽ���ɵõ����ۣ�
��� �⣺��1��300�£�180��1.5��=2.5��Сʱ����
�𣺼׳���A�ص���B�ص���ʻʱ����2.5Сʱ��
��2����׳�����ʱy��x֮��ĺ�����ϵʽΪy=kx+b��
��$\left\{\begin{array}{l}{300=2.5k+b}\\{0=5.5k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-100}\\{b=550}\end{array}\right.$��
��׳�����ʱy��x֮��ĺ�����ϵʽ��y=-100x+550��2.5��x��5.5����
��3��300��[��300-180����1.5]=3.75Сʱ��
��x=3.75ʱ��y=175ǧ�ף�
���ҳ�����A��ʱ�׳���A�ص�·����175ǧ�ף�
���� ���⿼���˴���ϵ����һ�κ����Ľ���ʽ�����ã��г������������ϵ�����ã����ʱ���һ�κ����Ľ���ʽ�ǹؼ���


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һ�Ÿ�����Ʊ�����صȽ� | |
| B�� | ��һ��������ѹ�£�����ˮ��100�棬���� | |
| C�� | ���������ε��ڽǺ�Ϊ180�� | |
| D�� | ��һ����װ�Ű���ͺ���Ĵ����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
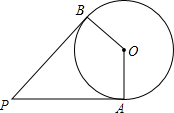 ��ͼ��PA��PB�ǡ�O�����ߣ��е�ֱ�ΪA��B����OA=2����P=60�㣬��$\widehat{AB}$�ij�Ϊ��������
��ͼ��PA��PB�ǡ�O�����ߣ��е�ֱ�ΪA��B����OA=2����P=60�㣬��$\widehat{AB}$�ij�Ϊ��������| A�� | $\frac{2}{3}$�� | B�� | �� | C�� | $\frac{4}{3}��$ | D�� | $\frac{5}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
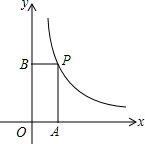 ��ͼ����ƽ��ֱ������ϵ�У���P�Ƿ���������y=$\frac{k}{x}$��x��0��ͼ���ϵ�һ�㣬�ֱ����P��PA��x���ڵ�A��PB��y���ڵ�B�����ı���OAPB�����Ϊ3����k��ֵΪ��������
��ͼ����ƽ��ֱ������ϵ�У���P�Ƿ���������y=$\frac{k}{x}$��x��0��ͼ���ϵ�һ�㣬�ֱ����P��PA��x���ڵ�A��PB��y���ڵ�B�����ı���OAPB�����Ϊ3����k��ֵΪ��������| A�� | 3 | B�� | -3 | C�� | $\frac{3}{2}$ | D�� | -$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��4 | C�� | 2��x��4 | D�� | x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3��x��5 | B�� | 3��x��5 | C�� | 3��x��-5 | D�� | -3��x��5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com