
如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
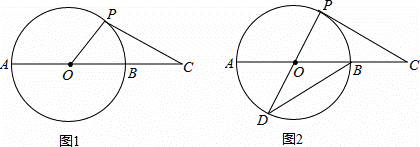
(1)解:∵AB=4,
∴OB=2,OC=OB+BC=4.
在△OPC中,设OC边上的高为h,
∵S△OPC= OC•h=2h,
OC•h=2h,
∴当h最大时,S△OPC取得最大值.
观察图形,当OP⊥OC时,h最大,如答图1所示:
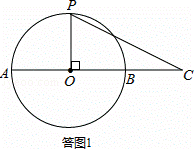
此时h=半径=2,S△OPC=2×2=4.
∴△OPC的最大面积为4.
(2)解:当PC与⊙O相切时,∠O CP最大.如答图2所示:
CP最大.如答图2所示:
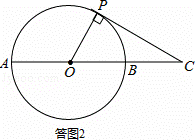
∵tan∠OCP= =
= =
= ,
,
∴∠OCP=30°
∴∠OCP的最大度数为30°.
(3)证明:如答图3,连接AP,BP.

∴∠A=∠D=∠APD=∠ABD,
∵ =
=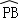 ,
,
∴ =
= ,
,
∴AP=BD,
∵CP=DB,
∴AP=CP,
∴∠A=∠C
∴∠A=∠D=∠APD=∠ABD∠C,
在△ODB与△BPC中
 ,
,
∴△ODB≌△BPC(SAS),
∴∠D=∠BPC,
∵PD是直径,
∴∠DBP=90°,
∴∠D+∠BPD=90°,
∴∠BPC+∠BPD=90°,
∴DP⊥PC,
∵DP经过圆心,
∴PC是⊙O的切线.


科目:初中数学 来源: 题型:
如图,经 过刨平的木板上的两个点,能弹出一条笔直的墨线,而
过刨平的木板上的两个点,能弹出一条笔直的墨线,而
|
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
利用对称变换可设计出美丽图案,如图,在方格纸中有一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出四边形关于直线l成轴对称的图形,再将你所作的图形和原四边形绕0点按顺时针旋转90°;
(2)完成上述图案设计后,可知这个图案的面积等于 20 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,将一个边长为a的 正方形纸片剪去两个小矩形,得到一个“
正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )

|
| A. | 2a﹣3b | B. | 4a﹣8b | C. | 2a﹣4b | D. | 4a﹣10b |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知梯形ABCD,请使用无刻度直尺画图.
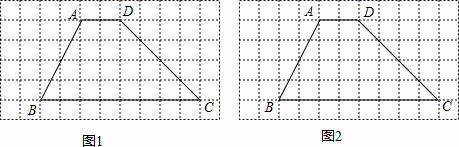
(1)在图1中画出一个与梯形ABCD面积相等,且以CD为边的三角形;
(2)图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校举办“成语听写大赛”,15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是 (填“平均数”或“中位数”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com