
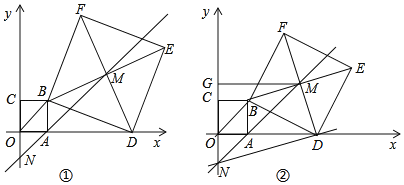
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
【答案】(1)详见解析;(2)详见解析;(3)N点的坐标为(0,﹣1);(4)D点坐标为(3,0).
【解析】
试题(1)根据题中给出的损矩形的定义,从图找出只有一组对角是直角的四边形即可;
(2)证明四边形BADM四个顶点到BD的中点距离相等即可;
(3)利用同弧所对的圆周角相等可得∠MAD=∠MBD,进而得到OA=ON,即可求得点N的坐标;
(4)根据正方形的性质及损矩形含有的直角,利用勾股定理求解.
(1)四边形ABMD为损矩形;
(2)取BD中点H,连结MH,AH
∵四边形OABC,BDEF是正方形
∴△ABD,△BDM都是直角三角形
∴HA=![]() BD HM=
BD HM=![]() BD
BD
∴HA=HB=HM=HD=![]() BD
BD
∴损矩形ABMD一定有外接圆
(3)∵损矩形ABMD一定有外接圆⊙H
∴![]() MAD =
MAD =![]() MBD
MBD
∵四边形BDEF是正方形
∴![]() MBD=45°
MBD=45°
∴![]() MAD=45°
MAD=45°
∴![]() OAN=45°
OAN=45°
∵OA=1
∴ON=1
∴N点的坐标为(0,-1)
(4) 延长AB交MG于点P,过点M作MQ⊥![]() 轴于点Q
轴于点Q
设MG=![]() ,则四边形APMQ为正方形
,则四边形APMQ为正方形
∴PM=AQ=![]() -1 ∴OG=MQ=
-1 ∴OG=MQ=![]() -1
-1
∵△MBP≌△MDQ
∴DQ=BP=CG=![]() -2
-2
∴MN2![]()
ND2![]()
MD2![]()
∵四边形DMGN为损矩形
∴![]()
![]()
![]()
∴![]()
∴![]() =2.5或
=2.5或![]() =1(舍去)
=1(舍去)
∴OD=3
∴D点坐标为(3,0).


科目:初中数学 来源: 题型:
【题目】如图,将边长为1的正三角形OAP沿χ轴方向连续翻转若干次,点P依次落在点P1,P2,P3,…,P2018的位置,则点P2018的横坐标为( )
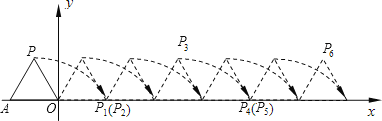
A.2016B.2017C.2018D.2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王某承包了甲、乙两片荒山,各栽了100棵杨梅树,现已全部挂果,为了分析收成情况,他分别从两山上各采摘了4棵树上的全部杨梅,每棵树的产量如折线统计图.
(1)分别计算甲、乙两山样本的平均数,并估计出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?

查看答案和解析>>
科目:初中数学 来源: 题型:
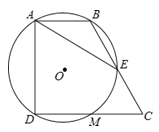
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:
①DM=CM;②弧AB=弧EM;③⊙O的直径为2;④AE=AD.
其中正确的结论有______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
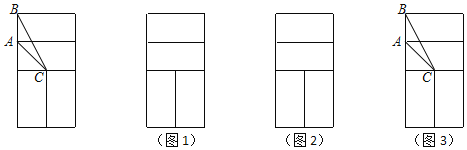
【题目】如图是四个全等的小矩形组成的图形,这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)
(1)若每个小矩形的较短边长为1,则BC= ;
(2)①在图1、图2中分别画一个格点三角形(顶点是格点的三角形),使它们都与△ABC相似(但不全等),且图1,2中所画三角形也不全等).
②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹,点M用黑点表示,并注上字母M)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,并且与边
,并且与边![]() 相切于点
相切于点![]() ,连接
,连接![]() .已知
.已知![]() 平分
平分![]() .
.
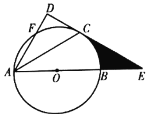
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 的半径为3.求阴影部分的面积.(结果保留
的半径为3.求阴影部分的面积.(结果保留![]() 和根号)
和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在![]() 中,
中,![]() ,
,![]() ,
,![]() , 动点
, 动点![]() 从点
从点![]() 出发以每秒3个单位的速度运动至点
出发以每秒3个单位的速度运动至点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() .
.
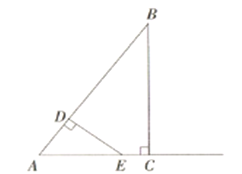
(1)线段![]() 长为 .(用含
长为 .(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() 与
与![]() 的面积比为1:4时, 求
的面积比为1:4时, 求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的周长为
重叠部分图形的周长为![]() , 求
, 求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,直接写出
分成的两部分图形中有一个是轴对称图形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合,就停止旋转.在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.
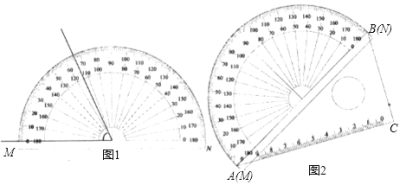
(1)设旋转x秒后,点E处的读数为y°,则y与x的函数关系式________.
(2)当CP旋转________秒时,△BCE是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com